A data model is a collection of conceptual tools for describing data, data relationships, data semantics, and consistency constraints. In this part, we focus on the relational model.
The relational model uses a collection of tables to represent both data and the relationships among the data. Its conceptual simplicity has led to its widespread adoption; today a vast majority of database products are based on the relational model. The relational model describes data at the logical and view levels, abstracting away low-level details of data storage.
1、Structure of Relational Databases
A relational database consists of a collection of tables, each of which is assigned a unique name. For example, consider the instructor table of Figure 2.1, which stores information about instructors. Similarly, the course table of Figure 2 stores information about courses, consisting of a course_id, title, dept_name, and credits, for each course.
Figure 1 The instructor relation.
Figure 2 The course relation
Figure 3 shows a third table, prereq, which stores the prerequisite courses for each course. The table has two columns, course_id and prereq_id. Each row consists of a pair of course identifiers such that the second course is a prerequisite for the first course.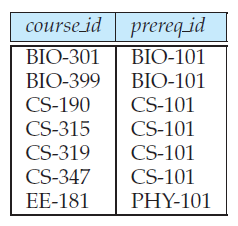
Figure 3 The prereq relation.
Thus, a row in the prereq table indicates that two courses are related in the sense that one course is a prerequisite for the other. As another example, we consider the table instructor, a row in the table can be thought of as representing the relationship between a specified ID and the corresponding values for name, dept_name, and salary values.
In general, a row in a table represents a relationship among a set of values. Since a table is a collection of such relationships, there is a close correspondence between the concept of table and the mathematical concept of relation, from which the relational data model takes its name. In mathematical terminology, a tuple is simply a sequence (or list) of values, i.e., a tuple with n values, which corresponds to a row in a table.
Thus, in the relational model the term relation is used to refer to a table, while the term tuple is used to refer a row. Similarly, the term attribute refers to a column of a table.
The order in which tuples appear in a relation is irrelevant, since a relation is a set of tuples. Thus, whether the tuples of a relation are listed in sorted order, as in Figure 1, or are unsorted, as in Figure 4, does not matter; the relations in the two figures are the same, since both contain the same set of tuples. For ease of exposition, we will mostly show the relations sorted by their first attribute.
Figure 4 Unsorted display of the instructor relation.
For each attribute of a relation, there is a set of permitted values, called the domain of that attribute. Thus, the domain of the salary attribute of the instructor relation is the set of all possible salary values, while the domain of the name attribute is the set of all possible instructor names.
We require that, for all relations r, the domains of all attributes of r be atomic. A domain is atomic if elements of the domain are considered to be indivisible units. The important issue is not what the domain itself is, but rather how we use domain elements in our database. Suppose now that the phone_number attribute stores a single phone number. Even that, if we split the value from the phone number attribute into a country code, an area code and a local number, we would be treating it as a nonatomic value. If we treat each phone number as a single indivisible unit, then the attribute phone_number would have an atomic domain.
The null value is a special value that signifies that the value is unknown or does not exist. We shall see later that null values cause a number of difficulties when we access or update the database, and thus should be eliminated if at all possible.
2、Database Schema
When we talk about a database, we must differentiate between the database schema, which is the logical design of the database, and the database instance, which is a snapshot of the data in the database at a given instant in time.
The concept of a relation corresponds to the programming-language notion of a variable, while the concepts of a relation schema corresponds to the programming-language notion of type definition.
In general, a relation schema consists of a list of attributes and their corresponding domains. The concept of a relation instance corresponds to the programming-language notion of a value of a variable. The value of a given variable may change with time; similarly the contents of a relation instance may change with time as the relation is updated. In contrast, the schema of a relation does not generally change.
Figure 5 The department relation.
Although it is important to know the difference between a relation schema and a relation instance, we often use the same name, such as instructor, to refer to both the schema and the instance. Where required, we explicitly refer to the schema or to the instance, for example “the instructor schema,” or “an instance of the instructor relation.” However, where it is clear whether we mean the schema or the instance, we simply use the relation name.
Consider the department relation of Figure 5. The schema for that relation is ![]()
Note that the attribute dept_name appears in both the instructor schema and the department schema. This duplication is not a coincidence. Rather, using common attributes in relation schemas is one way of relating tuples of distinct relations. For example, suppose we wish to find the information about all the instructors who work in the Watson building. We look first at the department relation to find the dept_name of all the departments housed in Watson. Then, for each such department, we look in the instructor relation to find the information about the instructor associated with the corresponding dept_name.
Let us continue with our university database example.
Each course in a university may be offered multiple times, across different semesters, or even within a semester. We need a relation to describe each individual offering, or section, of the class. The schema is ![]()
Figure 6 shows a sample instance of the section relation.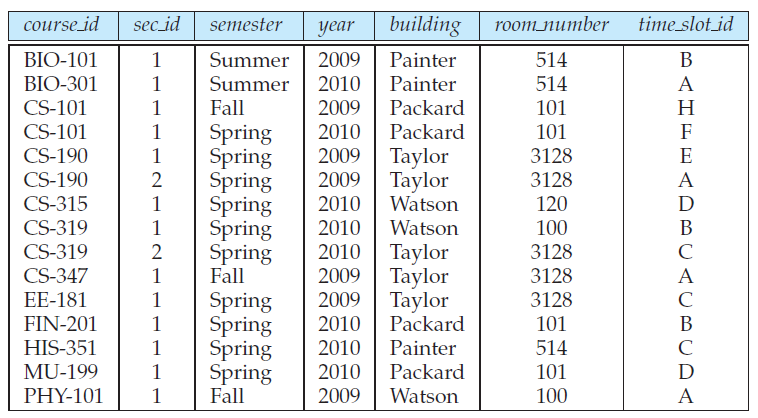
Figure 6 The section relation
We need a relation to describe the association between instructors and the class sections that they teach. The relation schema to describe this association is ![]()
Figure 7 shows a sample instance of the teaches relation. As you can imagine, there are many more relations maintained in a real university database. In addition to those relations we have listed already, instructor, department, course, section, prereq, and teaches, we use the following relations in this text:
Figure 7 The teaches relation.
- student (ID, name, dept_name, tot_cred)
- advisor (s_id, i_id)
- takes (ID, course_id, sec_id, semester, year, grade)
- classroom (building, room_number, capacity)
- time_slot (time_slot_id, day, start_time, end_time)
3、Keys
We must have a way to specify how tuples within a given relation are distinguished. This is expressed in terms of their attributes. That is, the values of the attribute values of a tuple must be such that they can uniquely identify the tuple. In other words, no two tuples in a relation are allowed to have exactly the same value for all attributes.
A superkey is a set of one or more attributes that, taken collectively, allow us to identify uniquely a tuple in the relation. For example, the ID attribute of the relation instructor is sufficient to distinguish one instructor tuple from another. Thus, ID is a superkey. The name attribute of instructor, on the other hand, is not a superkey, because several instructors might have the same name.
Formally, let R denote the set of attributes in the schema of relation r. If we say that a subset K of R is a superkey for r, we are restricting consideration to instances of relations r in which no two distinct tuples have the same values on all attributes in K. That is, if t1 and t2 are in r and t1 ≠ t2, then t1.K ≠ t2.K.
A superkey may contain extraneous attributes. For example, the combination of ID and name is a superkey for the relation instructor. If K is a superkey, then so is any superset of K. We are often interested in superkeys for which no proper subset is a superkey. Such minimal superkeys are called candidate keys.
It is possible that several distinct sets of attibutes could serve as a candidate key. Suppose that a combination of name and dept_name is sufficient to distinguish among members of the instructor relation. Then, both {ID} and {name, dept_name} are candidate keys. Although the attributes ID and name together can distinguish instructor tuples, their combination, {ID, name}, does not form a candidate key, since the attribute ID alone is a candidate key.
We shall use the term primary key to denote a candidate key that is chosen by the database designer as the principal means of identifying tuples within a relation. A key (whether primary, candidate, or super) is a property of the entire relation, rather than of the individual tuples. Any two individual tuples in the relation are prohibited from having the same value on the key attributes at the same time. The designation of a key represents a constraint in the real-world enterprise being modeled.
Primary keys must be chosen with care. As we noted, the name of a person is obviously not sufficient, because there may be many people with the same name. The primary key should be chosen such that its attribute values are never, or very rarely, changed.
It is customary to list the primary key attributes of a relation schema before the other attributes; for example, the dept_name attribute of department is listed first, since it is the primary key. Primary key attributes are also underlined.
A relation, say r1, may include among its attributes the primary key of another relation, say r2. This attribute is called a foreign key from r1, referencing r2. The relation r1 is also called the referencing relation of the foreign key dependency, and r2 is called the referenced relation of the foreign key. For example, the attribute dept_name in instructor is a foreign key from instructor, referencing department, since dept_name is the primary key of department. In any database instance, given any tuple, say ta, from the instructor relation, there must be some tuple, say tb, in the department relation such that the value of the dept_name attribute of ta is the same as the value of the primary key, dept_name, of tb.
Now consider the section and teaches relations. It would be reasonable to require that if a section exists for a course, it must be taught by at least one instructor; however, it could possibly be taught by more than one instructor. To enforce this constraint, we would require that if a particular (course_id, sec_id, semester, year) combination appears in section, then the same combination must appear in teaches. However, this set of values does not form a primary key for teaches, since more than one instructor may teach one such section. As a result, we cannot declare a foreign key constraint from section to teaches (although we can define a foreign key constraint in the other direction, from teaches to section).
The constraint from section to teaches is an example of a referential integrity constraint; a referential integrity constraint requires that the values appearing in specified attributes of any tuple in the referencing relation also appear in specified attributes of at least one tuple in the referenced relation.
4、Schema Diagrams
A database schema, along with primary key and foreign key dependencies, can be depicted by schema diagrams. Figure 8 shows the schema diagram for our university organization. Each relation appears as a box, with the relation name at the top in blue, and the attributes listed inside the box. Primary key attributes are shown underlined. Foreign key dependencies appear as arrows from the foreign key attributes of the referencing relation to the primary key of the referenced relation.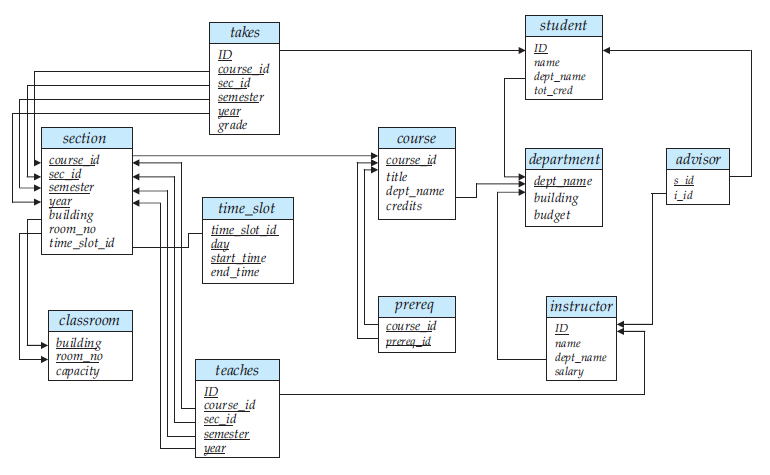
Figure 8 Schema diagram for the university database.
Referential integrity constraints other than foreign key constraints are not shown explicitly in schema diagrams. The enterprise that we use in the examples in later chapters is a university. Figure 2.9 gives the relational schema that we use in our examples, with primary-key attributes underlined. 
Figure 9 Schema of the university database.
5、Relational Query Languages
A query language is a language in which a user requests information from the database. These languages are usually on a level higher than that of a standard programming language. Query languages can be categorized as either procedural or nonprocedural. In a procedural language, the user instructs the system to perform a sequence of operations on the database to compute the desired result. In a nonprocedure language, the user describes the desired information without giving a specific procedure for obtaining that information.
Query languages used in practice include elements of the procedural and the nonprocedural approaches. There are a number of “pure” query languages: The relational algebra is procedural, whereas the tuple relational calculus and domain relational calculus are nonprocedural. These query languages are terse and formal, lacking the “syntactic sugar” of commercial languages, but they illustrate the fundamental techniques for extracting data from the database.
6、Relational Operations
All procedural relational query languages provide a set of operations that can be applied to either a single relation or a pair of relations. These operations have the nice and desired property that their result is always a single relation. This property allows one to combine several of these operations in a modular way. Specifically, since the result of a relational query is itself a relation, relational operations can be applied to the results of queries as well as to the given set of relations.
The most frequent operation is the selection of specific tuples from a single relation (say instructor) that satisfies some particular predicate (say salary > $85000). The result is a new relation that is a subset of the original relation (instructor).
Figure 10 Result of query selecting instructor tuples with salary greater than $85000.
Another frequent operation is to select certain attributes (columns) from a relation. The result is a new relation having only those selected attributes. For example, suppose we want a list of instructor IDs and salaries without listing the name and dept_name values from the instructor relation of Figure 1, then the result, shown in Figure 11, has the two attributes ID and salary. Each tuple in the result is derived from a tuple of the instructor relation but with only selected attributes shown.
Figure 11 Result of query selecting attributes ID and salary from the instructor relation.
The join operation allows the combining of two relations by merging pairs of tuples, one from each relation, into a single tuple. There are a number of different ways to join relations. Figure 12 shows an example of joining the tuples from the instructor and department tables with the new tuples showing the information about each instructor and the department in which she working. The result was formed by combing each tuple in the instructor relation with the tuple in the department relation for the instructor’s department.
In the form of join shown in Figure 12, which is called a natural join, a tuple from the instructor relation matches a tuple in the department relation if the values of their dept_name attributes are the same. All such matching pairs of tuples are present in the join result. In general, the natural join operation on two relations matches tuples whose values are the same on all attribute names that are common to both relations.
The Cartesian product operation combines tuples from two relations, but unlike the join operation, its result contains all pairs of tuples from the two relations, regardless of whether their attribute values match.
Because relations are sets, we can perform normal set operations on relations. The union operation performs a set union of two “similarly structured” tables. Other set operations, such as intersection and set difference can be performed as well.
As we noted earlier, we can perform operations on the results of queries. Sometimes, the result of a query contains duplicate tuples. Of course, data in a database must be changed over time. A relation can be updated by inserting new tuples, deleting existing tuples, or modifying tuples by changing the values of certain attributes. Entire relations can be deleted and new ones created.
RELATIONAL ALGEBRA
The relational algebra defines a set of operations on relations, paralleling the usual algebraic operations such as addition, subtraction or multiplication, which operate on numbers. Just as algebraic operations on numbers take one or more numbers as input and return a number as output, the relational algebra operations typically take one or two relations as input and return a relation as output. We outline a few of the operations below.
We shall discuss relational queries and updates using the SQL language later.
7、Summary
- The relational data model is based on a collection of tables. The user of the database system may query these tables, insert new tuples, delete tuples, and update(modify) tuples. There are several languages for expressing these operations.
- The schema of a relation refers to its logical design, while an instance of the relation refers to its contents at a point in time. The schema of a database and an instance of a database are similarly defined. The schema of a relation includes its attributes, and optionally the types of the attributes and constraints on the relation such as primary and foreign key constraints.
- A superkey of a relation is a set of one or more attributes whose values are guaranteed to identify tuples in the relation uniquely. A candidate key is a minimal superkey, that is, a set of attributes that forms a superkey, but none of whose subsets is a superkey. One of the candidate keys of a relation is chosen as its primary key.
- A foreign key is a set of attributes in a referencing relation, such that for each tuple in the referencing relation, the values of the foreign key attributes are guaranteed to occur as the primary key value of a tuple in the referenced relation.
- A schema diagram is a pictorial depiction of the schema of a database that shows the relations in the database, their attributes, and primary keys and foreign keys.
- The relational query languages define a set of operations that operate on tables, and output tables as their results. These operations can be combined to get expressions that express desired queries.
- The relational algebra provides a set of operations that take one or more relations as input and return a relation as an output. Practical query languages such as SQL are based on the relational algebra, but add a number of useful syntactic features.
