Before beginning to consider tree-processing algorithms, we continue in a mathematical vein by considering a number of basic properties of trees. We focus on binary trees, because we use them frequently throughout this series.
1、Mathematical Properties of Binary Trees
Understanding their basic properties will lay the groundwork for understanding the performance characteristics of various algorithms that we will encounter——not only of those that use binary trees as explicit data structures, but also of divide-and-conquer recursive algorithms and other similar applications.
Property 1 A binary tree with N internal nodes has N + 1 external nodes.
We prove this property by induction: A binary tree with no internal nodes has one external node, so the property holds for N = 0. For N > 0, any binary tree with N internal nodes has k internal nodes in its left subtree and N – 1 – k internal nodes in its right subtree for some k between 0 and N – 1, since the root is an internal node. By the inductive hypothesis, the left subtree has k + 1 external nodes and the right subtree has N – k external nodes, for a total of N + 1.
Property 2 A binary tree with N internal nodes has 2N links: N – 1 links to internal nodes and N + 1 links to external nodes.
In any rooted tree, each node, except the root, has a unique parent, and every edge connects a node to its parent, so there are N – 1 links connecting internal nodes. Similarly, each of the N + 1 external nodes has one link, to its unique parent. The performance characteristics of many algorithms depend not just on the number of nodes in associated trees, but on various structural properties.
Definition 1 The level of a node in a tree is one higher than the level of its parent (with the root at level 0). The height of a tree is the maximum of the levels of the tree’s nodes. The path length of a tree is the sum of the levels of all the tree’s nodes. The internal path length of a binary tree is the sum of the levels of all the tree’s internal nodes. The external path length of a binary tree is the sum of the levels of all the tree’s external nodes.
A convenient way to compute the path length of a tree is to sum, for all k, the product of k and the number of nodes at level k.
These quantities also have simple recursive definitions that follow directly from the recursive definitions of trees and binary trees. For example, the height of a tree is 1 greater than the maximum of the height of the subtrees of its root, and the path length of a tree with N nodes is the sum of the path lengths of the subtrees of its root plus N – 1. The quantities also relate directly to the analysis of recursive algorithms. For example, for many recursive computations, the height of the corresponding tree is precisely the maximum depth of the recursion, or the size of the stack needed to support the computation.
Property 3 The external path length of any binary tree with N internal nodes is 2N greater than the internal path length.
We could prove this property by induction, but an alternate proof (which also works for Property 2) is instructive. Observe that any binary tree can be constructed by the following process: Start with the binary tree consisting of one external node. Then, repeat the following N times: Pick an external node and replace it by a new internal node with two external nodes as children. If the external node chosen is at level k, the internal path length is increased by k, but the external path length is increased by k + 2 (one external node at level k is removed, but two at level k + 1 are added).
Property 4 The height of a binary tree with N internal nodes is at least lg N and at most N – 1.
The worst case is a degenerate tree with only one leaf, with N – 1 links from the root to the leaf (see Figure 1). The best case is a balanced tree with 2(i) internal nodes at every level i except the bottom level (see Figure 1). If the height is h, then we must have![]() since there are N + 1 external nodes. This inequality implies the property stated: The best-case height is precisely equal to lg N rounded up to the nearest integer.
since there are N + 1 external nodes. This inequality implies the property stated: The best-case height is precisely equal to lg N rounded up to the nearest integer.
Property 5 The internal path length of a binary tree with N internal nodes is at least N lg(N/4) and at most N(N – 1)/2.
The worst case and the best case are achieved for the same trees referred to in the discussion of Property 4 and depicted in Figure 1. The internal path length of the worst-case tree is 0 + 1 + 2 + … + (N + 1) = N(N – 1) / 2. The best case tree has (N + 1) external nodes at height no more than ⌊lg N⌋. Multiplying these and applying Property 3, we get the bound (N + 1)⌊lg N⌋ – 2N < Nlg(N/4).
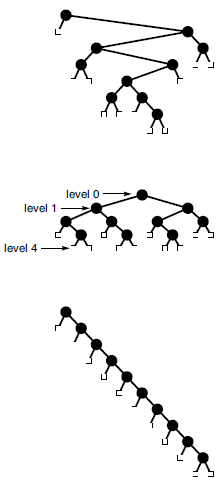 Figure 1 Three binary trees with 10 internal nodes
Figure 1 Three binary trees with 10 internal nodes
The binary tree shown at the top has height 7, internal path length 31 and external path length 51. A fully balanced binary tree (center) with 10 internal nodes has height 4, internal path length 19 and external path length 39 (no binary tree with 10 nodes has smaller values for any of these quantities). A degenerate binary tree (bottom) with 10 internal nodes has height 10, internal path length 45 and external path length 65 (no binary tree with 10 nodes has larger values for any of these quantities).
As we shall see, binary trees appear extensively in computer applications, and performance is best when the binary trees are fully balanced (or nearly so). For example, the trees that we use to describe divide-and-conquer algorithms such as binary search and mergesort are fully balanced. These basic properties of trees provide the information that we need to develop efficient algorithms for a number of practical problems. More detailed analyses of several of the specific algorithms that we shall encounter require sophisticated mathematical analysis, although we can often get useful estimates with straightforward inductive arguments like the ones that we have used in this section.
2、Tree Traversal
Before considering algorithms that construct binary trees and trees, we consider algorithms for the most basic tree-processing function: tree traversal: Given a pointer to a tree, we want to process every node in the tree systematically. In a linked list, we move from one node to the next by following the single link; for trees, however, we have decisions to make, because there may be multiple links to follow.
We begin by considering the process for binary trees. For linked lists, we had two basic options (see Program 5 in Recursion and Trees~ Recursive Algorithms): process the node and then follow the link (in which case we would visit the nodes in order), or follow the link and then process the node (in which case we would visit the nodes in reverse order). For binary trees, we have two links, and we therefore have three basic orders in which we might visit the nodes:
- Preorder, where we visit the node, then visit the left and right subtrees
- Inorder, where we visit the left subtree, then visit the node, then visit the right subtree
- Postorder, where we visit the left and right subtrees, then visit the node
We can implement these methods easily with a recursive program, as shown in Program 1, which is a direct generalization of the linked-list-traversal program in Program 5 in Recursion and Trees~ Recursive Algorithms. To implement traversals in the other orders, we permute the function calls in Program 1 in the appropriate manner. Figure 3 shows the order in which we visit the nodes in a sample tree for each other. Figure 2 shows the sequence of function calls that is executed when we invoke Program 1 on the sample tree in Figure 3.
Program 1 Recursive tree traversal
This recursive function takes a link to a tree as an argument and calls the function visit with each of the nodes in the tree as argument. As is, the function implements a preorder traversal; if we move the call to visit between the recursive calls, we have an inorder traversal; and if we move the call to visit after the recursive calls, we have a postorder traversal.
Figure 2 Preorder-traversal function calls
This sequence of function calls constitutes preorder traversal for the example tree in Figure 3. Figure 3 Tree-traversal orders
Figure 3 Tree-traversal orders
These sequences indicate the order in which we visit nodes for preorder (left), inorder (center), and postorder (right) tree traversal.
We have already encountered the same basic recursive processes on which the different tree-traversal method are based, in divide-and-conquer recursive programs (see Figure 6 and 9 in Recursion and Trees~ Divide and Conquer), and in arithmetic expressions. For example, doing preorder traversal corresponds to drawing the marks on the ruler first, then making the recursive calls (see Figure 9); doing inorder traversal corresponds to moving the biggest disk in the towers of Hanoi solution in between recursive calls that move all of the others; doing postorder traversal corresponds to evaluating postfix expressions, and so forth. These correspondences give us immediate insight into the mechanisms behind tree traversal. For example, we know that every other node in an inorder traversal is an external node, for the same reason that every other move in the towers of Hanoi problem involves the small disk.
It is also useful to consider nonrecursive implementations that use an explicit pushdown stack. For simplicity, we begin by considering an abstract stack that can hold items or trees, initialized with the tree to be traversed. Then, we enter into a loop, where we pop and process the top entry on the stack, continuing until the stack is empty. If the poped entity is an item, we visit it; if the popped entity is a tree, then we perform a sequence of push operations that depends on the desired ordering:
- For preorder, we push the right subtree, then the left subtree, and then the node.
- For inorder, we push the right subtree, then the node, and then the left subtree.
- For postorder, we push the node, then the right subtree, and then the left subtree.
We do not push null trees onto the stack. Figure 4 shows the stack contents as we use each of these three methods to traverse the sample tree in Figure 3. We can easily verify by induction that this method produces the same output as the recursive one for any binary tree.
Figure 4 Stack contents for tree-traversal algorithms
These sequences indicate the stack contents for preorder (left), inorder (center), and postorder (right) tree traversal (see Figure 3), for an idealized model of the computation, similar to the one that we used in Figure 2 in Recursion and Trees~ Divide and Conquer, where we put the item and its two subtrees on the stack, in the indicated order.
The scheme described in the previous paragraph is a conceptual one that encompasses the three traversal methods, but the implementations that we use in practice are slightly simpler. For example, for preorder, we do not need to push nodes onto the stack (we visit the root of each tree that we pop), and we therefore can use a simple stack that contains only one type of item (tree link), as in the nonrecursive implementation in Program 2. The system stack that supports the recursive program contains return addresses and argument values, rather than items and nodes, but the actual sequence in which we do the computations (visit the nodes) is the same for the recursive and the stack-based methods.
A fourth natural traversal strategy is simply to visit the nodes in a tree as they appear on the page, reading down from top to bottom and from left to right. This method is called level-order traversal because all the nodes on each level appear together, in order. Figure 5 shows how the nodes of the tree in Figure 3 are visited in level order.
Remarkably, we can achieve level-order traversal by substituting a queue for the stack in Program 2, as shown in Program 3. For preorder, we use a LIFO data structure; for level order, we use a FIFO data structure. These programs merit careful study, because they represent approaches to organizing work remaining to be done that differ in an essential way. In particular, level order does not correspond to a recursive implementation relates to the recursive structure of the tree.
Program 2 Preorder traversal (nonrecursive)
This nonrecursive stack-based function is functionally equivalent to its recursive counterpart, Program 1.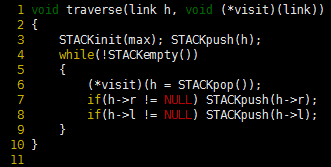
Program 3 Level-order traversal
Switching the underlying data structure in preorder traversal (see Program 2) from a stack to a queue transforms the traversal into a level-order one.
Figure 5 Level-order traversal
This sequence depicts the result of visiting nodes in order from top to bottom and left to right in the tree.
Preorder, postorder, and level order are well defined for forests as well. To make the definitions consistent, think of a forest as a tree with an imaginary root. Then, the preorder rule is “visit the root, then visit each of the subtrees,” the postorder rule is “visit each of the subtrees, then visit the root.” The level-order rule is the same as for binary trees. Direct implementations of these methods are straightforward generalizations of the stack-based preorder traversal programs (Program 1 and 2) and the queue-based level-order traversal program (Program 3) for binary trees that we just considered.
