最近正在研读Robert Sedgewick彻底修改和重写的C算法系列的第一本《算法:C语言实现(第1 – 4部分)基础知识、数据结构、排序及搜索》。该书细腻地讲解了计算机算法的C语言实现。徐徐研读,细细品味,偶有记录遂分享之!!!
一般而言,写程序的目的是为了实现事先设计的求解某个问题的方法。其重点在于如何解决问题的方法,而不在于使用某些特定的语言在特定计算机上写程序。算法用来描述适合于计算机程序实现的求解问题的方法。大多数算法关注的是计算机涉及的数据的组织方法。用此方法建立的对象称为数据结构(data structure)。故算法和数据结构就结合在一起了。
选择某个特定任务的最好算法可能是一个复杂的过程,也许涉及复杂的数学分析。分析表明经过研究的许多算法具有杰出的性能,还有一些算法经过实践表明可以很好地工作。我们的主要目的是学习求解重要任务的合理算法,然后还要仔细关注这些方法之间可比较的性能。不应该利用不清楚会消耗什么资源的算法,应努力了解我们到底期望我们的算法如何执行。
1、典型问题——连通性
假设给定整数对的一个序列,其中每个整数表示某种类型的一个对象,其中p~q表示“p连接到q”。假设“连通”关系是可传递的:即如果p和q之间连通,q和r之间连通,那么p和r也连通。以上描述归结为写一个过滤集合中的无关对的程序的问题。程序的输入为对p~q,如果已经看到的到那点的数对并不隐含着p连通到q,那么输出该对。如果前面的对确实隐含着p连通到q,那么程序应该忽略p~q,并应该继续输入下一对。下图给出了这个过程:
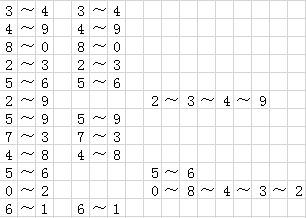
图 1 连通问题示例
注:给定表示两对象之间连接的整数对序列(左),连通算法的任务是输出那些提供新的连通关系的对(中间)。例如,由于连通关系2~3~4~9隐含在前面的数对中(右边给出了这个证明),因而对2~9不是输出的一部分。
上述问题表述为设计能够记录足够多它所看见的数对信息的程序,并能够判定一个新的对象对是否是连通的。通俗地称这样一个算法的任务为连通性问题。该问题出现在许多重要的应用中,比如计算机的大规模网络连接以及电网的连接等。
努力确定算法执行的基本操作很重要,这使为连通问题设计的算法可以用于许多类似的问题。确切的说,每当得到一个新对时,必须首先确定它是否表示一个新的连接,然后把已经看到的连接信息合并到已得到的对象的连通关系中,使得它能够检查将要看到的连接。此处可以将这两个任务封装成抽象操作,用整数输入值表示抽象集合中的元素,然后设计算法和数据结构,使其
- 查找(find)包含给定数据项的集合。
- 用它们的并集(union)替换包含两个给定数据项的集合。
按照这些抽象操作组织算法似乎并不妨碍求解连通性问题,并且这些操作可能用于求解其他问题。
利用查找和合并抽象操作可以容易地求解连通性问题。在从输入读取一个新的对p~q后,对于对中的每个数执行查找操作。如果对的成员在同一集合中,那么考虑下一对;如果它们不在同一集合中,则执行合并操作,并输出这个对。集合表示连通分量(connected component),即那些给定分量中的任何两个对象是连通的对象的集合。这种方法把开发连通问题算法解的过程变为定义表示集合的数据结构以及开发高效利用这个数据结构的查找和合并算法。
2、合并-查找算法
开发求解给定问题高效算法的过程的第一步是实现解这个问题的一个简单算法。如果要用更复杂的算法,简单实现可以用于检查小规模例子的正确性,并成为评估算法性能的一个基准。不要总是关注算法的效率,实际开发解决问题的第一个程序时更为关注的是确保程序的正确性。
2.1 快速-查找算法
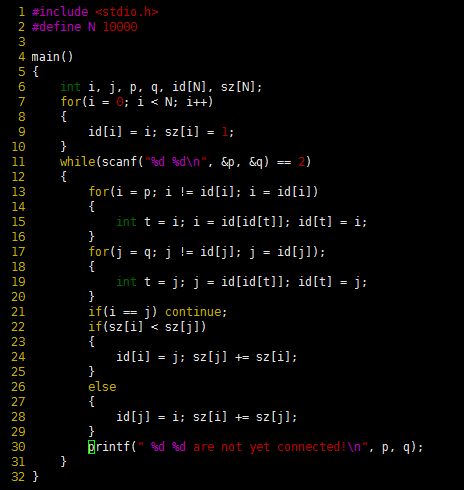
以下代码是求解连通问题的快速—查找算法(quick-find algorithm)的一种简单实现。算法的基础是一个整型数组,当且仅当第p个元素和第q个元素相等时,p和q是连通的。初始时,数组中的第i个元素的值为i,0≤ i <N。为实现p与q的合并操作,程序遍历数组,把所有名为p的元素值改为q。当然也可以把所有名为q的元素改为p。
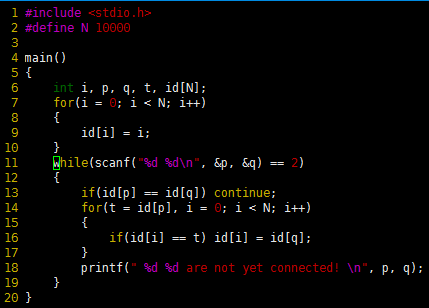
程序 1
该程序从标准输入读取小于N的非负整数对序列(对p~q表示“把对象p连接到q”),并且输出还未连通的输入对。程序中使用数组id,每个元素表示一个对象,且具有以下性质,当且仅当p和q是连通的,id[p]和id[q]相等。为简化起见,定义N为编译时的常数。另外也可以从输入得到它,并动态的为它分配id数组。代码编译、执行结果如下所示:
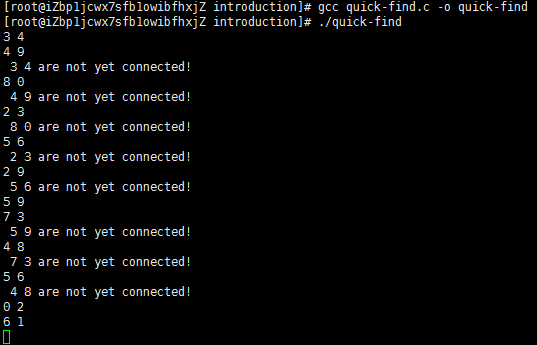
程序 1 编译执行结果
图 2 显示了对图 1 执行合并操作后的结果。为了实现查找操作,只需测试指示数组中的元素是否相等,故为快速查找。而合并操作对于每对输入需要扫描整个数组。
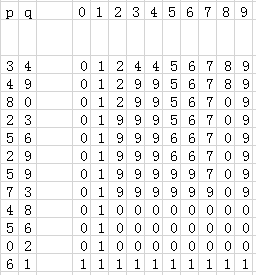
图 2 快速查找示例(慢速合并)
Property 1.1 The quick-find algorithm executes at least MN instructions to solve a connectivity problem with M pairs of N objects.
性质1.1 求解N个对象的连通性问题,如果执行M次合并操作,那么快速查找算法至少执行MN条指令。
对于每个合并操作,for循环迭代N次。每次迭代至少需要执行一次指令(如果只检测循环是否结束)。
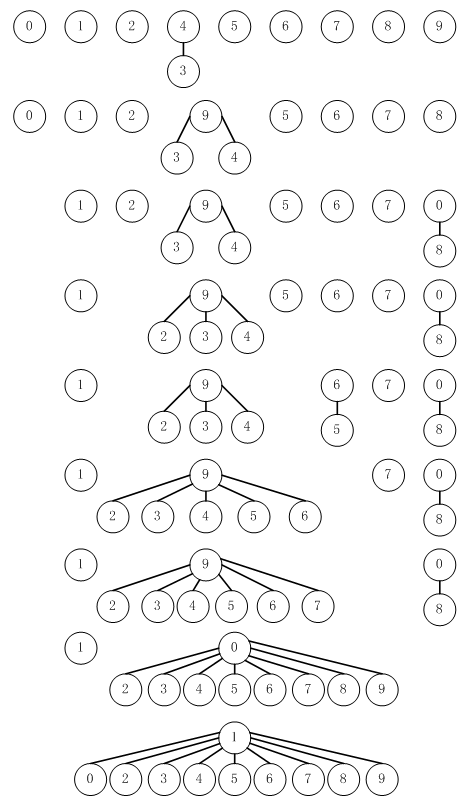
图 3 快速查找算法的树形表示
注:此图描述了图 2中示例的图形化表示。图中的连接并不一定表示输入中的连接。比如,最后一棵树的结构中有1~7这样的连接,它不在输入中,而是由连接7~3~4~9~5~6~1形成的。
图 3是图 2 的图形化表示。我们可以把某个对象看做它们所属集合的代表,其他所有对象指向它们所属集合的代表。用图形表示数组是由于对象之间的连接不必就是输入对的连接。它们是算法选择记住的一些信息,通过这些信息算法可以确定未来对是否是连通的。
2.2 快速-合并算法
它是基于同一个数据结构,即通过对象名引用数组元素,但数组元素表达的含义不同,具有更复杂的抽象结构。在一个没有环的结构中,每个对象指向同一集合中的另一个对象。要确定两个对象是否在同一集合中,只需跟随每个对象的指针,直到到达指向自身的一个对象。当且仅当这个过程使两个对象到达同一个对象时,这两个对象在同一个集合中。如果两者不在同一个集合中,最终一定到达不同对象(每个对象都指向自身)。为了构造合并操作,只需将一个对象链接到另一个对象以执行合并操作,故为快速-合并(quick-union)。
图 4 的图形化表示对应图 3,它是用快速合并算法执行图1示例的结果
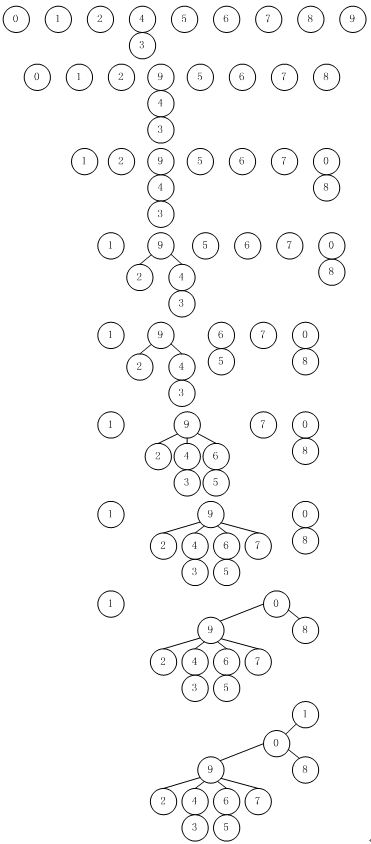
图 4 快速合并算法的树形表示
注:该图是图 2示例中的图形化表示。画了从对象i到对象id[i]的一条线。
图 5显示了id数组中的相应变化。数据结构的图形化表示利于相对容易地理解算法中的操作,即数据中已知是连通的输入对在数据结构中的对也是连通的。图 4描述的连通部分称为树。对于合并和查找操作,图 4 中的树是有用的,因为它们可以快速建立,并且有如下性质:当且仅当两个对象在输入中是连通时,这两个对象在树中连通。沿着树向上,可以很容易地找到包含每个对象的树的树根,于是我们就有了一种查找它们是否连通的方法。每棵树只有一个对象指向它自己,这个对象称为树的根(root)。当我们从树中的任一对象开始,并移到它指向的对象,然后移到那个对象指向的对象,如此这样,最终总会在根节点结束。
图 3 也具有上述性质,两者不同之处在于,在快速查找树中所有节点只需一个链接就可达树根,而在快速合并树中,可能要经过几个链接才能到达树根。
程序 2 是合并和查找操作的一种实现,它们包含了求解连通问题的快速合并算法。
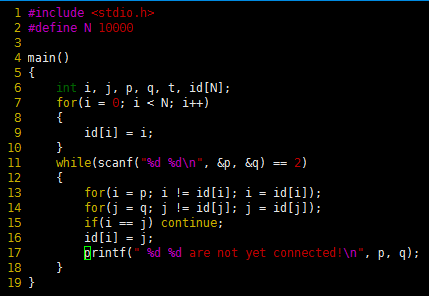
程序 2
程序 2 同样满足程序 1 中的说明,但其合并操作的计算时间较短,查找操作的计算时间更长。代码中的for循环以及if语句指明了在数组id中p和q是连通的充分必要条件。赋值语句id[i] = j实现合并操作。
通过实际运行或者进行数学分析,可以确信程序 2 比程序 1 有效得多,且对于大规模实际问题程序 2 更可行。可以认为快速合并算法是一种改进,它去掉了快速查找的主要局限性(对N个对象执行M次合并操作,程序至少需要MN条指令)。但快速合并算法仍然具有局限性,我们不能保证每种情况下,它都会比快速查找算法要快,因为输入数据可能使查找操作变慢。
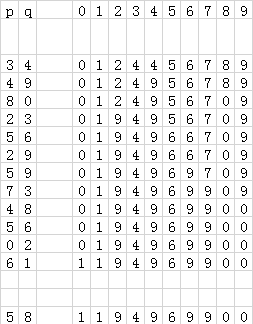
图 5 快速合并算法示例(不太快的查找)
注:这个序列描述了快速合并算法(程序 2)在左边每对上执行后id数组中的内容变化情况。当处理对p~q时,沿着从p开始的指针到达id[i] == i的元素i;然后沿着从q开始的指针到达id[j] == j的元素j;如果i和j不等,则设id[i] = id[j]。对于最后一行的对5~8的查找操作,i的取值为5 6 9 0 1,j的取值为8 0 1.
Property 1.2 For M > N, the quick-union algorithm could take more than MN/2 instructions to solve a connectivity problem with M pairs of N objects.
性质1.2 对于M > N,快速合并算法求解 N 个对象,M个对的连通问题需要执行 MN/2条指令。
假定输入对按照1~2,2~3,3~4,……的次序出现。N-1个这样的输入对之后,可得N个对象都在同一个集合中,且快速合并算法形成的树是一条直线,其中N指向N-1,N-1指向N-2,N-2指向N-3,依次类推。要在对象N上执行查找操作,程序必须遍历N-1个指针。故对前N个对遍历的平均指针数为
(0+1+…+(N-1)) / N = (N – 1) / 2
现在假设其余对都把N连接到某个对象。每对进行查找操作至少访问N-1个指针。故在这个输入对序列上执行M个查找操作访问的指针总数必定大于MN/2。
2.3 加权快速合并算法
幸运的是,简单修改算法就可以保证不会出现这样的最坏情况。在合并操作中,不是任意地把第二课树连接到第一棵树上,而是记录每棵树中的节点数,总是把较小的树连接到较大的树上。这种修改只增加一点代码,需要另一数组保存节点计数,如程序3所示。但其结果导致效率上的巨大改进。该算法称为加权快速合并算法(weighted quick-union).
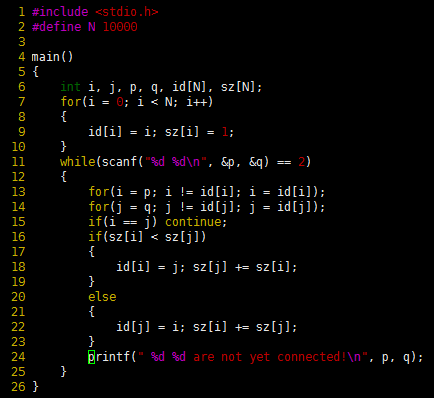 程序 3
程序 3
图 6 显示了加权合并-查找算法对于图 1中输入示例所构造的树的森林。即使是个较小例子,树中的路径要比图4中未加权的快速合并算法要短得多。图 7 说明了当合并操作中待归并集合的大小总是相等时,出现最坏情况。这些树结构看起来复杂,但它们具有简单性质,即在一颗2n个节点的树中,到达根节点需要遍历的指针数为n。进一步说,当归并节点数为2n的两棵树时,可以得到2n+1个节点的树。到根节点的最大距离增加到n+1。概括这个观察结果,可得加权快速合并算法比未加权的算法更高效的一个证明。
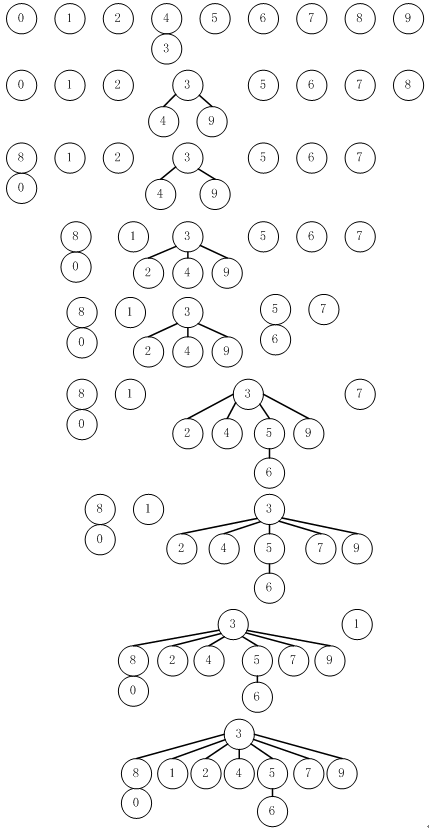
图 6 加权快速合并算法的树形表示
注:这个序列描述了将快速合并算法改为把两棵树中较小树的树根连接到较大树的树根上的结果。这棵树中每个节点到根节点的距离变小,因而查找操作更高效。
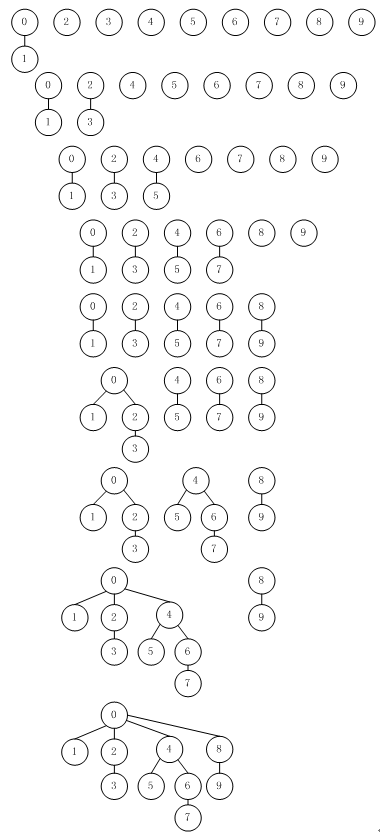
图 7 加权快速合并算法(最坏情况)
注:加权快速合并算法的最坏情况出现在每次合并操作连接大小相等的两棵树。如果对象个数小于2n,那么从任一节点到树的根节点的距离小于n。
Property 1.3 The weighted quick-union algorithm follows at most lg N pointers to determine whether two of N objects are connected.
性质 1.3 对于N个对象,加权快速合并算法判定其中的两个对象是否是连通的,至多需要遍历lg N个指针。
可以证明合并操作维持了性质:在一个k个对象的集合中,从任一节点到达根节点所访问的指针数不大于lg k(没有计算指向自己的根节点的指针)。当合并i个节点的一个集合与j个节点的一个集合时,且i ≤ j,把必须遍历的i个节点的集合中的指针数增1,但这些指针现在在大小为i + j的集合中,于是1 + lg i = lg(i + i)≤ lg(i+ j)可得性质成立。
实际实现性质1.3时,加权快速合并算法至多利用M lg N条指令处理N个对象的M条边。与早先快速查找算法至少利用MN/2条指令相比,这个结果好很多。
由图可见,相对少的节点距根节点较远。实际上,大规模问题的实验研究表明程序3中的加权快速合并算法可在线性(linear)时间求解实际问题。即运行算法所需时间是读取输入时间的常数倍数。
2.4 路径压缩
能否找到一个保证线性性能的算法???理想情况下,希望每个节点直接指向其根节点,但又不希望像在快速合并算法中所指的那样,花费代价修改大量指针。我们可以简单地使检查的所有节点指向树的根节点。这一步看似不切实际,却容易通过修改树的结构实现。这种方法称之为路径压缩(path compression)。
在合并操作过程中,添加经过每条路径的另一个指针,使沿路遇见的每个顶点对应的id元素指向树的根节点。结果是几乎使树完全平扁,接近快速查找算法达到的理想情况,如图8所示。
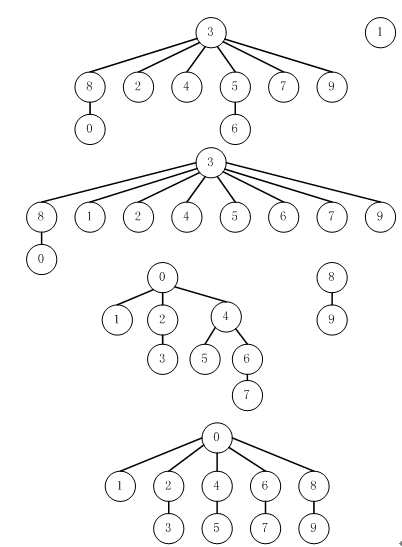
图 8
注:我们可以使树中的路径更短,在合并操作中使所有访问的对象指向新树的根节点。如这两个例子中所示。上面的例子对应图6的结果。对于较短路径,路径压缩没有作用,当我们处理对1~6时,使1、5和6都指向3,并得到一棵比图6更扁的一棵树。下面的例子对应图7的结果。长于1或2个链接的路径可以扩展,但无论何时遍历它们,都使它们平扁。当处理对6~8时,通过使4、6和8都指向0使树平扁。
还有许多方法可以实现路径压缩。如程序 4 所示是一种实现,它通过使每条链接跳跃到树中向上的路径的下一个节点实现压缩,如图 9 所示。这种方法比完全路径压缩实现起来稍微容易一些,并能达到同样的结果,该方法称之为带有等分路径压缩的加权快速-合并算法。
3、 总结及展望
文中考虑的每个算法似乎是对以前版本的一种改进,但是该过程需要人工修饰。因为实现简单且问题明确,因此可以通过实验研究直接评价各种算法。更进一步,我们可以验证这些实验,并量化地比较这些算法的性能。并不是所有的问题都可以像连通性问题这样改进,后续必定会遇见一些难以比较的复杂算法,还会遇见难以求解的数学问题。只要可能,在实际设计其他算法时都应沿用合并-查找算法的基本步骤,主要步骤如下:
- 确定完整、明确的问题陈述,包括确定问题固有的基本抽象操作。
- 仔细设计一个简单算法的简明实现。
- 通过逐步求精的过程开发改进后的实现,经过实验分析、数学分析或者两者共同验证改进思想的效率。
- 找出数据结构或者算法操作的高级抽象表示,能够使改进版本的设计高效。
- 可能时尽量保证最坏情况下的性能,但实际数据可用时接受好的性能。
开发一个高效算法是一项满足智力且有实际回报的活动。正如在连通问题中所阐明的,一个简单的问题不仅可以研究许多既有用又有趣的算法,而且也有复杂和难以理解的算法。在科学计算和商业问题的应用领域,能够高效算法解决已知问题和研究新问题变得越来越重要。
