Organizing the data for processing is an essential step in the development of a computer program. For many applications, the choice of the proper data structure is the only major decision involved in the implementation: once the choice has been made, the necessary algorithms are simple.
A data structure is not a passive object: We also must consider the operations to be performed on it (and the algorithms used for these operations). This concept is formalized in the notion of a data type.
1. Building Blocks
Types allow us to specify how we will use particular sets of bits and functions allow us to specify how we will use particular that we will perform on the data. We use C structures to group together heterogeneous pieces of information, and we use pointers to refer to information indirectly. In this section, we consider these basic C mechanisms, in the context of presenting a general approach to organizing our programs. Our primary goal is to lay the groundwork for the development of the higher-level constructs that will serve as the basis for most of the algorithms.
We write programs that process information derived from mathematical or natural-language descriptions of the world in which we live; accordingly, computing environments provide built-in support for the basic building blocks of such descriptions — numbers and characters. In C, our programs are all built from just a few basic types of data:
- Integers (ints).
- Floating-point numbers (floats).
- Characters (chars).
Characters are most often used in higher-level abstractions — for example to make words and sentences — so we defer consideration of character data to later section and look at numbers here.
We use a fixed number of bits to represent numbers, so ints are by necessity integers that fall within a specific range that depends on the number of bits that we use to represent them. Floating-point numbers approximate real numbers, and the number of bits that we use to represent the affects the precision with which we can approximate a real number. In C, we trade space for accuracy by choosing from among the types int, long int, or short int for integers and from among float or double for floating-point numbers.
In modern programming, we think of the type of the data more in terms of the needs of the program than the capabilities of the machine, primarily, in order to make programs portable. Thus, for example, we think of an int (short int is 16-bit in 32-bit machine, int and short int is 16-bit in 16-bit machine)as an object that can take on values between -32767 and 32767, instead of as a 16-bit object.
Definition 1 A data type is a a set of values and a collection of operations on these values.
Operations are associated with types, not the other way around. When we perform an operation, we need to ensure that its operands and result are of the correct type. Neglecting this responsibility is a common programming error. In some situations, C performs implicit type conversions; In other situations, we use casts, or explicit type conversions. For example, if x and N are integers, the expression
((float) x) / N
includes both types of conversion: the (float) is a cast that converts the value of x to floating point; then an implicit conversion is performed for N to make both arguments of the divide operator floating point, according to C’s rules for implicit type conversion.
Indeed, in a sense, each C program is a data type — a list of sets of values(built-in or other types) and associated operations (functions). This point of view is perhaps too broad to be useful, but we shall see that narrowing our focus to understand our programs in terms of data types is valuable.
Program 1 Function definition
The mechanism that we use in C to implement new operation on data is the function definition, illustrated here.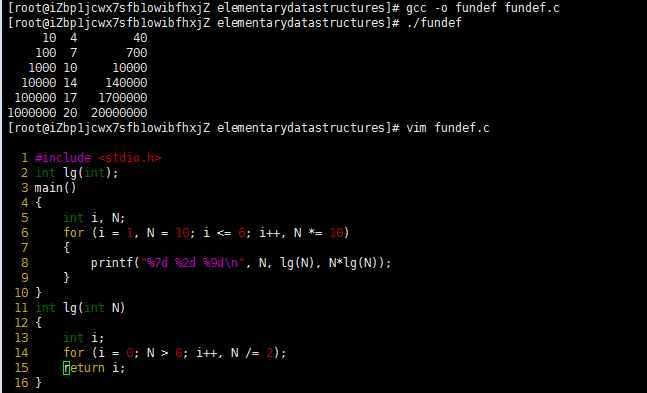
All functions have a list of arguments and possibly a return value. The function lg here has one argument and a return value, each of type integer. The function main has neither arguments nor return values.
We declare the function by giving its name and the types of its return values. The first line of code here references a system file that contains declarations of system functions such as printf. The second line of code is a declaration for lg. The declaration is optional if the function is defined before it is used, as is the case with main. The declaration provides the information necessary for other functions to call or invoke the function, using argument of the proper type. The calling program can use the function in an expression, in the same way as it uses variables of the return-value type.
We define functions with C code. All C programs include a definition of the function main, and this code also defines lg. In a function definition, we give names to the arguments (which we refer to as parameters), and express the computation in terms of those names, as if they were local variables. When the function is invoked, these variables are initialized with the values of the arguments and the function code is executed. The return statement is the instruction to end execution of the function and provide the return value to the calling program. In principle, the calling program is not to be otherwise affected, though we shall see many exceptions to this principle.
The separation of definition and declaration provides flexibility in organizing programs. For example, both could be in separate files. Or, in a simple program like this one, we could put the definition of lg before the definition of main and omit its declaration.
One goal that we have when writing programs is to organize them such that they apply to as broad a variety of situations as possible. The reason for adopting such a goal is that it might put us in the position of being able to reuse an old program to solve a new problem, perhaps completely unrelated to the problem that the program was originally intended to solve. First, by taking care to understand and to specify precisely which operations a program uses, we can easily extend it to any type of data for which we can support those operations. Second, by taking care to understand and to specify precisely what a program does, we can add the abstract operation that it performs to the operations at our disposal in solving new problems.
Program 2 Types of numbers
This program computes the average μ and standard deviation σ of a sequence
of integers generated by the library procedure rand, following the mathematical definitions
Note that a direct implementation from the definition of σ² requires one pass to compute the average and another to compute the sums of the squares of the differences between the members of the sequence and average, but rearranging the formula makes it possible for us to compute σ² in one pass through the data.
We use the typedef declaration to localize reference to the fact that the type of the data is int. For example, we could keep the typedef and the function randNum in a separate file (referenced by an include directive), and then we could use this program to test random numbers of a different type by changing that file.
Whatever the type of the data, the program uses ints for indices and floats to compute the average and standard deviation, and will be effective only if conversion functions from the data to float perform in a reasonable manner.
It is worthwhile to consider in detail how we might change the data type to make Program 2 work with other types of numbers, say floats, rather than with ints. There are a number of different mechanisms available in C that we could use to take advantage of the fact we have localized references to the type of the data. For such a small program, the simplest is to make a copy of the file, then to change the typedef to
typedef float numType;
and the procedure randNum to
return 1.0*rand（）/ RAND_MAX;
(which will return random floating-point numbers between 0 and 1). Even for such a small program, this approach is inconvenient because it leaves us with two copies of the main program, and we will have to make sure that any later changes in that program are reflected in both copies. In C, an alternative approach is to put the typedef and randNum into a separate head file — called, say, Num.h — replacing them with directive
#include “Num.h”
A third alternative, which is recommended software engineering practice, is to split the program into three files:
- An interface, which defines the data structure and declares the functions to be used to manipulate the data structure
- An implementation of the functions declared in the interface
- A client program that use the functions declared in the interface to work at a higher level of abstraction
We think of the interface as a definition of the data type. It is a contract between the client program and the implementation program. The client agrees to access the data only through the functions defined in the interface, and the implementation agrees to deliver the promised functions.
For the example in Program 2, the interface would consist of the declarations
The fourth line specifies the type of the data to be processed, and the fifth specifies operations associated with the type. This code might be kept, for example, in a file named Num.h.
The implementation of the interface in Num.h is an implementation of the randNum function, which might consist of the code
The first line refers to the system-supplied interface that describes the rand() function; The fourth line refers to the interface that we are implementing (we include it as a check that the function we are implementing is the same type as the one that we declared), and the final four lines give the code for the function. This code might be kept, for example, in a file named int.c. The actual code for the rand function is kept in the standard C run-time library.
A client program corresponding to Program 2 would begin with the include directives for interfaces that declare the functions that it uses, as follows:
The function main from Program 2 then can follow these included files. The code might be kept, for example in a file named avg.c.
Compiled together, the programs avg.c and int.c describe in the previous paragraphs have the same functionality as Program 2, but they represent a more flexible implementation both because the code associated with the data type is encapsulated and can be used by other client programs and because avg.c can be used with other data types without being changed.
There are many other ways to support data types besides the client-interface-implementation scenario just described, but we will not dwell on distinctions among various alternatives because such distinctions are best drawn in a systems-programming context, rather than in an algorithm-design context (see reference section). However, we do often make use of this basic design paradigm because it provides us with a natural way to substitute improved implementations for old ones, and therefore to compare different algorithms for the same applications problem.
We often want to build data structures that allow us to handle collections of data. The data structures may be huge, or they may be used extensively, so we are interested in identifying the important operations that we will perform on the data and in knowing how to implement those operations efficiently. Doing these tasks is taking the first steps in the process of incrementally building lower-level abstractions into higher-level ones; that process allows us to conveniently develop ever more powerful programs. The simplest mechanisms for grouping data in an organized way in C are arrays and structures.
Structures are aggregate types that we use to define collections of data such that we can manipulate an entire collection as a unit, but can still refer to individual components of a given datum by name. Structures are not at the same level as built-in types such as int or float in C, because the only operations that are defined for them (beyond referring to their components) are copy and assignment. Thus, we can use a structure to define a new type of data, and can use it to name variables, and can pass those variables as arguments to functions, but we have specifically to define as functions any operations that we want to perform.
Program 3 Point data type interface
This interface defines a data type consisting of the set of values “pairs of floating-point numbers” and the operation consists of a function that computes the distance between two points.
Program 4 Point data type implementation
This implementation provides the definition for the distance function for points that is declared in Program 3. It makes use of a library function to compute the square root.
Program 3 is an interface that embodies the definition of a data type for points in the plane, uses a structure to represent the points, and includes an operation to compute the distance between two points. Program 4 is a function that implements the operation. We use interface-implementation arrangements like this to define data types whenever possible, because they encapsulate the definition (in the interface) and the implementation in a clear and direct manner. We make use of the data type in a client program by including the interface and by compiling the implementation with the client program (or by using appropriate separate-compilation facilities). Program 3 uses a typedef to define the point data type so that client programs can declare points as point instead of struct point, and do not have to make any assumptions about how the data types are represented.
We cannot use Program 2 to process items of type point because arithmetic and type conversion operations are not defined for points. Modern languages such as C++ and Java have basic constructs that make it possible to use previously defined high-level abstract operations, even for newly defined types. With a sufficiently general interface, we could make these arrangements, even in C. Our primary goal is to make clear the effectiveness of the algorithmic ideas the we will be considering. Although we often stop short of a fully general solution, we do pay careful attention to the process of precisely defining the abstract operations that we want to perform, as well as the data structures and algorithms that will support those operation, because doing so is at the heart of developing efficient and effective programs.
Beyond giving us the specific basic types int, float, and char, and the ability to build them into compound types with struct, C provides us with the ability to manipulate our data indirectly. A pointer is a reference to an object in memory (usually implemented as a machine address). We declare a variable a to be a pointer to (for example) an integer by writing int *a, and we can refer to the integer itself as *a. We can declare pointers to any type of data. The unary operator & gives the machine address of an object, and is useful for initializing pointers. For example, *&a is the same as a. We restrict ourselves to using & for this purpose, as we prefer to work at a somewhat higher level of abstraction than machine addresses when possible.
Referring to an object indirectly via a pointer is often more convenient than referring directly to the object, and can also be more efficient, particularly for large objects. Even more important, as we shall see, we can use pointers to structure our data in ways that support efficient algorithms for processing the data. Pointers are the basis for many data structures and algorithms.
A simple and important example of the use of pointers arises when we consider the definition of a function that is to return multiple values. For example, the following function (using the functions sqrt and atan2 from the standard library) converts from Cartesian to polar coordinates:
In C, all function arguments are passed by value —— if the function assigns a new value to an argument variable, that assignment is local to the function and is not seen by the calling program. This function therefore cannot change the pointers to the floating-point numbers r and theta, but it can change the values of the numbers, by indirect reference. For example, if a calling program has a declaration float a, b, the function call
will result in a being set to 1.414214 (√2) and b being set to 0.785398 (π/4). The & operator allows us to pass the addresses of a and b to the function, which treats those arguments as pointers. We have already seen an example of this usage, in the scanf library function.
So far, we have primarily talked about defining individual pieces of information for our programs to process. In many instances, we are interested in working with potentially huge collections of data, and we now turn to basic methods for doing so. In general, we use the term data structure to refer to a mechanism for organizing our information to provide convenient and efficient mechanisms for accessing and manipulating it. Many important data structures are based on one or both of the two elementary approaches that we shall consider in next article. We may use an array, where we organize objects in a fixed sequential fashion that is more suitable for access than for manipulation; or a list, where we organize objects in a logical sequential fashion that is more suitable for manipulation than for access.