在前文 信号完整性小记 ~ 概述 中指出分析和表征信号完整性，分为时域和频域两种途径和手段。时域是根本，可以用示波器观察信号波形的失真和眼图，找出 pin-to-pin 的时延、错位、抖动、噪声、过冲/下冲及建立/保持时间等，选用的仪器有 TDR（Time Domain Reflectometry）。频域是用频谱分析仪观察分析信号的波形，通常用于信号噪声的带宽分析、噪声抑制度量及 EMI 量级分析，仪器有 VNA 和 阻抗分析仪 IA
1、时域与频域分析方法
1.1 时域分析方法
时域是真实存在的，可以在时域分析信号的幅度和时序，所有时序波形的优劣对比都是在时域中观察和验证的。
时钟波形除了电压幅度之外，还有两个重要的参数：即时钟周期与上升时间。上升时间的定义有两种：一种是默认的：10%~90%的上升时间，另一种是20~80%上升时间。时域波形中下降沿的定义通常也是10~90%和20~80%。下降沿通常比上升沿短，这是由于典型 CMOS 输出驱动器设计造成的。
1.2 频域分析方法
频域一般不对应真实的物理对象，它是一种虚构的数学变换形式。正弦波是频域中唯一真实存在的波形，这是傅里叶频域最重要的优秀特征。人们可以用熟悉的正弦波在傅里叶频域完成对电压和电流波形的方便又等价的描述。
频域中并不产生新的信息，同一波形的时域或频域所含的信息完全等价。
1.3 傅里叶变换
为了实现在频域的分析和处理，需要将波形从时域变换到频域，傅里叶变换就是这样的工具，傅里叶变换有三种：
⑴ 傅里叶积分（FI）
傅里叶积分将时间轴上从 -∞ 到 +∞ 的积分，得到的结果是从零频率到 +∞ 频率上连续的频域函数。
⑵ 傅里叶级数（FS）
对于时域周期函数，对应频域中是离散函数，这就是傅里叶级数。
则 f(t) 的FS式为：
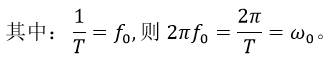
f(t)可以理解为ω0的各次谐波nω0分量之和，每个分量都有不同幅度和初相。
⑶ 离散傅里叶变换（DFT）及其快速算法（FFT）
如果时域波形具有周期性，可以用一系列离散点采样值加以表征，称作时域周期离散函数。对应于频域也是离散周期函数，这就是离散傅里叶变换，对应快速算法是 FFT。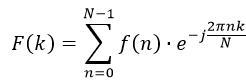
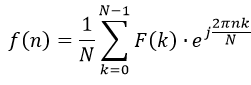
One cycle of a 1-GHz clock signal in the time domain (top) and frequency domain (bottom).
2、时域信号与频谱
2.1 理想方波的傅立叶级数
理想方波信号的上升时间为零，占空比为50%，假设幅值为 1V，如上图所示。如果假设此信号的频率为 1GHz，那么频谱中的正弦波频率就是 1GHz 的整数倍。可以采用 DFT 的方法计算出各频率分量的幅值，也有一种相对简单的方式来确定各次谐波的幅值。即：
An 即为谐波的幅值系数，用 An 乘以方波的幅值即为谐波的幅值，如当方波为 1V 时，一次谐波的幅值为 0.63V，三次谐波的幅值为 0.21V，幅值随幂函数 1/f 的减小而减小。
2.2 频域正弦级数合成时域信号波形
频谱表示的是时域波形包含的所有正弦波频率的幅度，如果已知一个时域波形的频谱，把每个频率分量变换成它的时域波形，再将其线性叠加，就可得到时域波形，这就是傅里叶级数合成的逆变换，如下图所示：
Convert the frequency-domain spectrum into the time-domain waveform by adding up each sine-wave component.
对于 1V，1GHz 的理想方波的频谱，第一项是零次谐波，幅度为 0.5V，此分量描述了时域中的直流常量。第二个分量是一次谐波，在时域中是频率为 1GHz，幅度为 0.63V 的正弦波。一次谐波与零次谐波叠加，得到幅值均值为 0.5V的正弦波，如下图所示。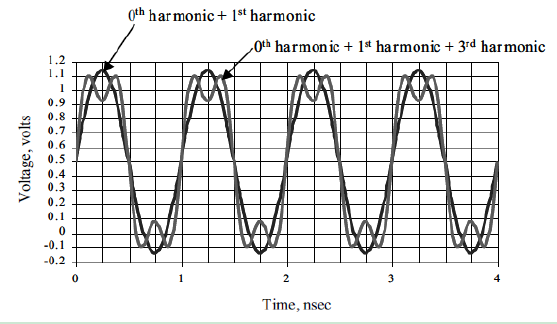
The time-domain waveform is created by adding together the zeroth harmonic and first harmonic and then the third harmonic, for a 1-GHz ideal square wave.
此波形与理想方波差距较大，当叠加了三次谐波之后，时域波形的上升边沿开始变得陡峭。把所有相继的高次谐波不断与已有波形相叠加，得到的结果会越来越像理想方波。尽管高频分量的幅值已经很低，但又不可忽视，通常认为信号完整性研究的是宽带信号。
The time domain waveform created by adding together the zeroth harmonic and first harmonic, then the third harmonic and then up to the seventh harmonic, then up to the nineteenth harmonic, and then all harmonics up to the thirty-first harmonic, for a 1-GHz ideal square wave.
3、信号带宽与信号上升沿
3.1 信号带宽与上升沿之间的关系
输入信号经过传输线变成输出信号，可用时域上升沿描述，也可用频域带宽来描述，两者是等价的。如果能够找出频谱带宽与时域上升沿之间的关系将是很有帮助的，经过对波形的 10~90%上升沿和带宽的波形测量，可以画一个简单的关系式，这个关系式对所有信号均适用，如下图所示：
Empirical relationship between the bandwidth of a signal and its 10-90 rise time, as measured from a re-created ideal square wave with each harmonic added one at a time. Circles are the values extracted from the data; line is the approximation of BW = 0.35/rise time.
通过拟合之后发现信号带宽与信号上升沿之间呈现倒数关系，如下式所示：
此处的带宽是指信号的最高频率。
3.2 一般信号的带宽
信号带宽定义为信号的最高有效正弦波分量，最高有效分量是指高于这个点的信号谐波分量幅度比理想方波中相应频率的幅度小到某种程度，如常用的3dB，即为功率下降 50%，电压下降 70%。下面是一个理想方波与上升时间为0.08ns 的梯形波的对比图，从图中可以看出，一次和三次谐波两者大致相同，而梯形波的五次谐波分量幅值大约是理想方波五次谐波电压值的 70%，七次谐波只有理想方波的 30%。由波形图可知，梯形波频谱中有效的最高正弦波频率分量是五次谐波，即梯形波的带宽为5GHz，如果用前面的公式估算带宽为：
BW = 0.35/0.08 = 4.4GHz
可见带宽本身是一种近似，完整的频谱图才是对时域波形的频域最精确表示。
Top: Time domain waveforms of 1-GHz repeat frequency: an ideal square wave and an ideal trapezoidal wave with 0.08-nsec rise time. Bottom: Frequency-domain spectra of these waveforms showing the drop-off of the trapezoidal wave’s
3.3 有振铃时的信号带宽
如果传输线路的终端匹配不好，则会发生振铃现象，在振铃频率处频谱出现峰值。振铃频率处的幅值比没有振铃时信号的幅度高 10 倍以上，如下图所示：
Top: The time-domain waveform of a near-square wave and one that has significant ringing due to poor termination. Bottom: the resulting DFT spectrum of these two waves, showing the effect of the ringing on the spectrum. The wide bars are for the ideal waveform while the narrow bars are for the ringing waveform.
信号的电磁干扰（EMI）的总辐射随着频率而线性增加，谐波幅度以 1/f 速率下降，所以，各次谐波对 EMI 的影响大致相同。电路中若有了振铃，此时的带宽约等于振铃频率。高频分量幅度将提高 10 倍以上，再加上频率又高，使得辐射强度增加很多，为了减少 EMI， 一定要解决 SI 问题。为了减少 EMI，所有信号在设计时采用尽量低的带宽。
3.4 高速与高频的关系
信号的带宽与其上升沿有关，与信号的频率没有直接的关系。如果仅要从信号的频率去估计其带宽，需要估计任意一个波形的典型上升时间，即信号上升时间与周期的比值。一个典型的估计是上升沿时间是周期的7%，根据之前的公式就可得出时钟带宽是信号频率的5倍。这样高速信号与高频信号取得了模糊的一致。
4、信号的互联
4.1 互联本征带宽与本征上升沿
本征上升沿是指理想方波信号通过互连之后实际输出上升沿变差的情况，本征带宽是指理想方波经互联损耗后输出信号的最高有效正弦波频率分量（如 3dB带宽）。上述二参数是时域频域的不同表征，是完全一致的。
输出的频率分量减少了3dB，即电压幅度减少为输入值的70%，这就是互连 3dB带宽。互连的带宽可以在时域中测量，主要还是在频域中测量。下图为正弦波通过 FR4 板上 10cm 长， 50欧姆的传输线时所测得的幅度值，由图可知，互连的 3dB 带宽为 8GHz。
信号经过互联输出后其上升沿会变长，变化的大小与本征上升沿有关，可以使用下面的公式进行计算。
Measured transmitted amplitude of different sine-wave signals through a 4-inch-long transmission line made in FR4. The 3 dB bandwidth is seen to be about 8 GHz for this cross section and material properties. Measured with a Giga Test Labs Probe Station.
要使互连对信号的上升沿造成的增量不超过 10%，互联的本征上升沿就要小于该信号上升沿的 50%，这是个简单的经验法则。
从频域看，为了较好地传输带宽为 1GHz 的信号，互联的本征带宽应至少为信号的两倍，即 2GHz。