Of the data types that support insert and delete for collections of objects, the most important is called the pushdown stack.
1、Pushdown Stack ADT
A stack operates somewhat like a busy professor’s “in” box: work piles up in a stack, and whenever the professor has a chance to get some work done, it comes off the top. A student’s paper might well get stuck at the bottom of the stack for a day or two, but a conscientious professor might manage to get the stack emptied at the end of the week. As we shall see, computer programs are naturally organized in this way. They frequently postpone some tasks while doing others; moreover, they frequently need to return to the most recently postponed task first. Thus, pushdown stacks appear as the fundamental data structure for many algorithms.
Definition 1 A pushdown stack is an ADT that comprises two basic operation: insert (push) a new item, and delete (pop) the item that was most recently inserted.
That is, when we speak of a pushdown stack ADT, we are referring to a description of the push and pop operations that is sufficiently well specified that a client program can make use of them, and to some implementation of the operations enforcing the rule that characterizes a pushdown stack: items are removed according to a last-in, first-out (LIFO) discipline. In the simplest case, which we use most often, both client and implementation refer to just a single stack (that is, the “set of values” in the data type is just that one stack).
Figure 1 shows how a sample stack evolves through a series of push and pop operations. Each push increases the size of the stack by 1 and each pop decreases the size of the stack by 1. In the figure, the items in the stack are listed in the order that they are put on the stack, so that it is clear that the rightmost item in the list is the one at the top of the stack—the item that is to be returned if the next operation is pop. In an implementation, we are free to organize the items any way that we want, as long as we allow clients to maintain the illusion that the items are organized in this way.
Figure 1 Pushdown stack (LIFO queue) example
This list shows the result of the sequence of operations in the left column (top to bottom), where a letter denotes push and an asterisk denotes pop. Each time displays the operation, the letter popped for pop operations, and the contents of the stack after the operation, in order from least recently inserted to most recently inserted, left to right.
Program 1 Pushdown-stack ADT interface
This interface defines the basic operations that define a pushdown stack. We assume that the four declarations here are in a file STACK.h, which is referenced as an include file by client programs that use these functions and implementations that provide their code; and that both clients and implementations define Item, perhaps by including an Item.h file (which may have a typedef or which may define a more general interface). The argument to STACKinit specifies the maximum number of elements expected on the stack.
To write programs that use the pushdown stack abstraction, we need first to define the interface. In C, one way to do so is to declare the four operations that client programs may use, as illustrated in Program 1. We keep these declarations in a file STACK.h that is referenced as an include file in client programs and implementations.
Furthermore, we expect that there is no other connection between client programs and implementations. We have already seen the value of identifying the abstract operations on which a computation is based previously. We are now considering a mechanism that allow us to write programs that use these abstract operations. To enforce the abstraction, we hide the data structure and the implementation from the client.
In an ADT, the purpose of the interface is to serve as a contract between client and implementation. The function declarations ensure that the calls in the client program and the function definitions in the implementation match, but the interface otherwise contains no information about how the functions are to be implemented, or even how they are to behave. How can we explain what a stack is to a client program? For simple structures like stacks, one possibility is to exhibit the code, but this solution is clearly not effective in general. Most often, programmers resort to English-language descriptions, in documentation that accompanies the code.
A rigorous treatment of this situation requires a full description, in some formal mathematical notation, of how the functions are supposed to behave. Such a description is sometimes called a specification. Developing a specification is generally a challenging task. It has to describe any program that implements the functions in a mathematical metalanguage, whereas we are used to specifying the behavior of functions with code written in a programming language. In practice, we describe behavior in English-language description. Before getting drawn further into epistemological issues, we move on. In this series, we give detailed examples, English-language descriptions, and multiple implementations for most of the ADTs that we consider.
2、Examples of Stack ADT Clients
We shall see a great many applications of stacks in the series that follow. As an introductory example, we now consider the use of stacks for evaluating arithmetic expressions. For example, suppose that we need to find the value of a simple arithmetic expression involving multiplication and addition of integers, such as
The calculation involves saving intermediate results: For example, if we calculate 9 + 8 first, then we have to save the 17 while, say, we compute 4 * 6. A pushdown stack is the ideal mechanism for saving intermediate results in such a calculation.
We begin by considering a simpler problem, where the expression that we need to evaluate is in a form where each operator appears after its two arguments, rather than between them. As we shall see, any arithmetic expression can be arranged in this form, which is called postfix, by contrast with infix, the customary way of writing arithmetic expressions. The postfix representation of the expression in the previous paragraph is 
The reverse of postfix is called prefix, or Polish notation (because it was invented by the Polish logician Lukasiewicz). In infix, we need parentheses to distinguish, for example,from
but parentheses are unnecessary in postfix (or prefix). To see why, we can consider the following process for converting a postfix expression to an infix expression: We replace all occurrences of two operands followed by an operator by their infix equivalent, with parentheses, to indicate that the result can be considered to be an operand. That is, we replace any occurrence of a b * and a b + by (a * b) and (a + b), respectively. Then, we perform the same transformation on the resulting expression, continuing until all the operators have been processed. For our example, the transformation happens as follows: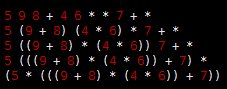
We can determine the operands associated with any operator in the postfix expression in this way, so no parentheses are necessary.
Alternatively, with the aid of a stack, we can actually perform the operations and evaluate any postfix expression, as illustrated in Figure 2. Moving from left to right, we interpret each operand as the command to “push the operand onto the stack,” and each operator as the commands to “pop the two operands from the stack, perform the operation, and push the result.” Program 2 in a C implementation of this process.
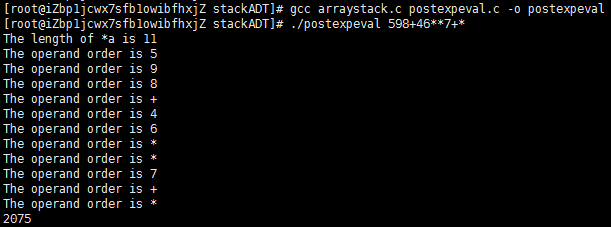
Figure 2 Evaluation of a postfix expression
This sequence shows the use of a stack to evaluate the postfix expression 5 9 8 + 4 6 * * 7 + *. Proceeding from left to right through the expression, if we encounter a number, we push it on the stack; and if we encounter an operator, we push the result of applying the operator to the top two numbers on the stack.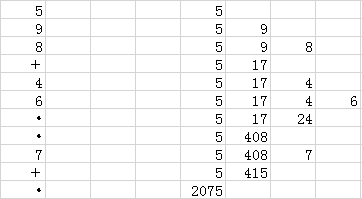
Program 2 Postfix-expression evaluation
This pushdown-stack client reads any postfix expression involving multiplication and addition of integers, then evaluates the expression and prints the computed result.
When we encounter operands, we push them on the stack; when we encounter operators, we pop the top two entries from the stack and push the result of applying the operator to them. The order in which the two STACKpop() operations are performed in the expressions in this code is unspecified in C, so the code for noncommutative operators such as subtraction or division would be slightly more complicated.
The program assumes that at least one blank follows each integer, but otherwise does not check the legality of the input at all. The final if statement and the while loop perform a calculation similar to the C atoi function, which converts integers from ASCII strings to integers for calculation. When we encounter a new digit, we multiply the accumulated result by 10 and add the digit. The stack contains integers—that is, we assume that Item is defined to be int in Item.h, and that Item.h is also included in the stack implementation.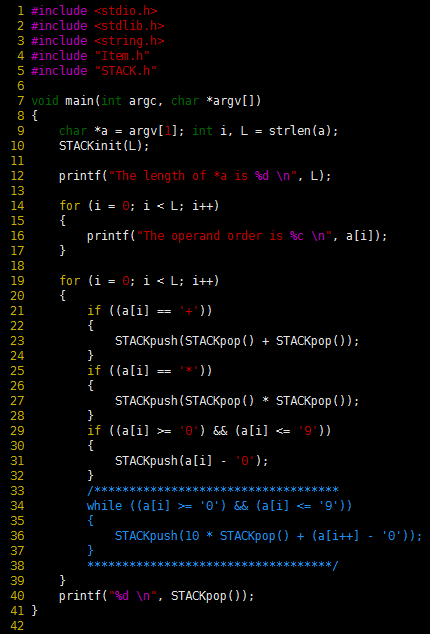
Postfix notation and an associated pushdown stack give us a natural way to organize a series of computational procedures. Some calculators and some computing language explicitly base their method of calculation on postfix and stack operations—every operations pops its arguments from the stack and return its results to the stack.
One example of such a language is the PostScript language, which is used to print the series. It is a complete programming language where programs are written in postfix and are interpreted with the aid of an internal stack, precisely as in Program 2. Although we cannot cover all the aspects of the language here, it is sufficiently simple that we can study some actual programs, to appreciate the utility of the postfix notation and the pushdown-stack abstraction. For example, the string
is a PostScript program! Programs in PostScript consist of operators (such as add and mul) and operands (such as integers). As we did in Program 2 we interpret a program by reading it from left to right: If we encounter an operand, we push it onto the stack; if we encounter an operator, we pop its operands (if any) from the stack and push the result (if any). Thus, the execution of this program is fully described by Figure 2: The program leaves the value 2075 on the stack.
PostScript has a number of primitive functions that serve as instructions to an abstract plotting device; we can also define our own functions. These functions are invoked with arguments on the stack in the same way as any other function. For example, the PostScript code 
corresponds to the sequence of actions “call moveto with arguments 0 and 0, then call hill with argument 144,” and so forth. Some operators refer directly to the stack itself. For example the operator dup duplicates the entry at the top of the stack so, for example, the PostScript code
corresponds to the sequence of actions “call rlineto with arguments 144 and 0, then call rotate with argument 60, then call rlineto with arguments 144 and 0,” and so forth. The PostScript program in Figure 3 defines and uses the function hill. Functions in PostScript are like macros: The sequence /hill { A } def makes the name hill equivalent to the operator sequence inside the braces. Figure 3 is an example of a PostScript program that defines a function and draws a simple diagram.
Figure 3 Sample PostScript program
The diagram at the top was drawn by the PostScript program below it. The program is a postfix expression that uses the built-in functions moveto, rlineto, rotate, stroke and dup; and the user-defined function hill (see text). The graphics commands are instructions to a plotting device: moveto instructs that device to go to the specified position on the page (coordinates are in points, which are 1/72 inch); rlineto instructs it to move to the specified position in coordinates relative to its current position, adding the line it makes to its current path; rotate instructs it to turn left the specified number of degrees; and stroke instructs it to draw the path that it has traced.
In the present context, our interest in PostScript is that this widely used programming language is based on the pushdown-stack abstraction. Indeed, many computers implement basic stack operations in hardware because they naturally implement a function-call mechanism: Save the current environment on entry to a function by pushing information onto a stack; restore the environment on exit by using information popped from the stack. This connection between pushdown stacks and programs organized as functions that call functions is an essential paradigm of computation.
Return to our original problem, we can also use a pushdown stack to convert fully parenthesized arithmetic expressions from infix to postfix, as illustrated in Figure 4. For this computation, we push the operator onto a stack, and simply pass the operands through to the output. Then, each right parenthesis indicates that both arguments for the last operator have been output, so the operator itself can be popped and output.
Figure 4 Conversion of an infix expression to postfix
This sequence shows the use of a stack to convert the infix expression (5*(((9+8)*(4*6))+7)) to its postfix from 5 9 8 + 4 6 * * 7 + * . We proceed from left to right through the expression: If we encounter a number, we write it to the output; if we encounter a left parenthesis, we ignore it; if we encounter an operator; we push it on the stack; and if we encounter a right parenthesis, we write the operator at the top of the stack to the output.
Program 3 Infix-to-postfix conversion
This program is another example of a pushdown-stack client. In this case, the stack contains characters—we assume that Item is defined to be char (that is, we use a different Item.h file than for Program 2). To convert (A+B) to the postfix from AB+, we ignore the left parenthesis, convert A to postfix, save the + on the stack, convert B to postfix, then on encountering the right parenthesis, pop the stack and output the +.
Program 3 is an implementation of this process. Note that arguments appear in the postfix expression in the same order as in the infix expression. It is also amusing to note that the left parentheses are not needed in the infix expression. The left parentheses would be required, however, if we could have operators that take differing numbers of operands.
In addition to providing two different examples of the use of the pushdown-stack abstraction, the entire algorithm that we have developed in this section for evaluating infix expressions is itself an exercise in abstraction. First, we convert the input to an intermediate representation (postfix). Second, we simulate the operation of abstract stack-based machine to interpret and evaluate the expression. This same schema is followed by many modern programming-language translators, for efficiency and portability: The problem of compiling a C program for a particular computer is broken into two tasks centered around an intermediate representation, so that the problem of translating the program is separated from the problem of executing that program, just as we have done in this section.
This application also illustrates that ADTs do have their limitations. For example, the conventions that we have discussed do not provide an easy way to combine Program 2 and 3 into a single program, using the same pushdown-stack ADT for both. Not only do we need two different stacks, but also one of the stacks holds single characters (operators), whereas the other holds numbers. To better appreciate the problem, suppose that the numbers are, say, floating-point numbers, rather than integers. Using a general mechanism to allow sharing the same implementation between both stacks is likely to be more trouble than simply using two different stacks. In fact, as we shall see, this solution might be the approach of choice, because different implementation may have different performance characteristics, so we might not wish to decide a priori that one ADT will serve both purposes. Indeed, our main focus is on the implementations and their performance, and we turn now to those topics for pushdown stacks.
3、Stack ADT Implementations
In this section, we consider two implementations of the stack ADT: one using arrays and one using linked lists. The implementations are both straightforward applications of the basic tools we covered before. They differ only, we expect, in their performance characteristics.
if we use an array to represent the stack, each of the functions declared in Program 1 is trivial to implement, as shown in Program 4. We put the items in the array precisely as diagrammed in Figure 1, keeping track of the index of the top of the stack. Doing the push operation amounts to storing the item in the array position indicated by the top-of-stack index, then incrementing the index; doing the pop operation amounts to decrementing the index, then returning the item that it designates. The initialize operation involves allocating an array of the indicated size, and the test if empty operation involves checking whether the index is 0. Compiled together with a client program such as Program 2 or Program 3, this implementation provides an efficient and effective pushdown stack.
Program 4 Array implementation of a pushdown stack
When there are N items in the stack, this implementation keeps them in s[0], …, s[N-1]; in order from least recently inserted to most recently inserted. The top of the stack (the position where the next item to be pushed will go) is s[N]. The client program passes the maximum number of items expected on the stack as the argument to STACKinit, which allocates an array of that size, but this code does not check for errors such as pushing onto a full stack (or popping an empty one).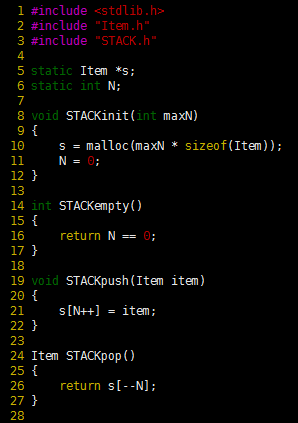
We know one potential drawback to using an array representation: As is usual with data structures based on arrays, we need to know the maximum size of the array before using it, so that we can allocate memory for it. In this implementation, we make that information an argument to the function that implements initialize. This constraint is an artifact of our choice to use an array implementation; it is not an essential part of the stack ADT. We may have no easy way to estimate the maximum number of elements that our program will be putting on the stack: If we choose an arbitrarily high value, this implementation will make inefficient use of space, and that may be undesirable in an application where space is a precious resource. If we choose too small value, our program might not work at all. By using an ADT, we make it possible to consider other alternatives, in other implementations, without changing any client program.
For example, to allow the stack to grow and shrink gracefully, we may wish to consider using a linked list, as in the implementation in Program 5. In this program, we keep the stack in reverse order from the array implementation, from most recently inserted element to least recently inserted element, to make the basic stack operations easier to implement, as illustrated in Figure 5. To pop, we remove the node from the front of the list and return its item; to push, we create a new node and add it to the front of the list. Because all linked-list operations are at the beginning of the list, we do not need to use a head node. This implementation does not need to use the argument to STACKinit.
Programs 4 and 5 are two different implementations for the same ADT. we can substitute one for the other without making any changes in client programs such as the ones that we examined before. They differ in only their performance characteristics—the time and space that they use. For example, the list implementation uses more time for push and pop operations, to allocate memory for each push and deallocate memory for each pop. If we have an application where we perform these operations a huge number of times, we might prefer the array implementation. On the other hand, the array implementation uses the amount of space necessary to hold the maximum number of items expected throughout the computation, while the list implementation uses space proportional to the number of items, but always uses extra space for on link per item. If we need a huge stack that is usually nearly full, we might prefer the array implementation; if we have a stack whose size varies dramatically and other data structures that could make use of the space not being used when the stack has only a few items in it, we might prefer the list implementation.
Figure 5 Linked-list pushdown stack
The stack is represented by a pointer head, which points to the first (most recently inserted) item. To pop the stack (top), we remove the item at the front of the list, by setting head from its link. To push a new item onto the stack (bottom), we link it in at the beginning by setting its link field to head, then setting head to point to it.
Program 5 Linked-list implementation of a pushdown stack
This code implements the stack ADT as illustrated in Figure 5. It uses an auxiliary function NEW to allocate the memory for a node, set its fields from the function arguments, and return a link to the node.
These same considerations about space usage hold for many ADT implementations as we shall see throughout the series. We often are in the position of choosing between the ability to access any item quickly but having to predict the maximum number of items needed ahead of time (in an array implementation) and the flexibility of always using space proportional to the number of items in use while giving up the ability to access every item quickly (in a linked-list implementation).
Beyond basic space-usage considerations, we normally are most interested in performance differences among ADT implementations that relate to running time. In this case, there is little difference between the two implementations that we have considered.
Property 1 We can implement the push and pop operations for the pushdown stack ADT in constant time, using either arrays or linked lists.
This fact follows immediately from inspection of Program 4 and 5.
That the stack items are kept in different orders in the array and the linked-list implementations is of no concern to the client program. The implementations are free to use any data structure whatever, as long as they maintain the illusion of an abstract pushdown stack. In both cases, the implementations are able to create the illusion of an efficient abstract entity that can perform the requisite operations with just a few machine instructions. Throughout the series, our goal is to find data structures and efficient implementations for other important ADTs.
The linked-list implementation supports the illusion of a stack that can grow without bound. Such a stack is impossible in practical terms: at some point, malloc will return NULL when the request for more memory cannot be satisfied. It is also possible to arrange for an array-based stack to grow dynamically, by doubling the size of the array when the stack becomes half empty.