Abstract Data Types~Stack ADT present a complete example of C code that captures one of our most important abstractions: the pushdown stack. The interface defines the basic operations; client programs can use those operations without dependence on how the operations are implemented; and implementations provide the necessary concrete representation and program code to realize the abstraction.
1、Creation of a New ADT
To design a new ADT, we often enter into the following process. Starting with the task of developing a client program to solve an applications problem, we identify operations that seem crucial: What would we like to be able to do with our data? Then, we define an interface and write client code to test the hypothesis that the existence of the ADT would make it easier for us to implement the client program. Next, we consider the idea of whether or not we can implement the operations in the ADT with reasonable efficiency. If we cannot, we perhaps can seek to understand the source of the inefficiency and to modify the interface to include operations that are better suited to efficient implementation. These modification affect the client program, and we modify it accordingly. After a few iterations, we have a working client program and a working implementation, so we freeze the interface: We adopt a policy of not changing it. At this moment, the development of client programs and the development of implementations are separable: We can write other client programs that use the same ADT (perhaps we write some driver programs that allow us to test the ADT), we can write other implementations, and we can compare the performance of multiple implementations.
In other situations, we might define the ADT first. This approach might involve asking questions such as these: What basic operations would client programs want to perform on the data at hand? Which operations do we know how to implement efficiently? After we develop an implementation, we might test its efficacy on client programs. We might modify the interface and do more tests, before eventually freezing the interface.
Program 1 Equivalence-relations ADT interface
The ADT interface mechanism makes it convenient for us to encode precisely our decision to consider the connectivity algorithm in terms of three abstract operations: initialize, find whether two nodes are connected, and perform a union operation to consider them connected henceforth.
Program 1 defines the interface, in terms of two operations (in addition to initialize) that seem to characterize the algorithms that we considered previous for connectivity, at a high abstract level. Whatever the underlying algorithms and data structures, we want to be able to check whether or not two nodes are known to be connected, and to declare the two nodes are connected.
Program 2 Equivalence-relations ADT client
The ADT of Program 1 separates the connectivity algorithm from the union-find implementation, making that algorithm more accessible.
Program 2 is a client program that uses the ADT defined in the interface of Program 1 to solve the connectivity problem. One benefit of using the ADT is that this program is easy to understand, because it is written in terms of abstractions that allow the computation to be expressed in a natural way.
Program 3 Equivalence-relation ADT implementation
This implementation of the weighted-quick-union code from previous section, together with the interface of Program 1, packages the code in a form that makes it convenient for use in other applications. The implementation uses a local function find.

Program 3 is an implementation of the union-find interface defined in Program 1 that uses a forest of trees represented by two arrays as the underlying representation of the known connectivity information, as described in previous section. The different algorithms that we consider represent different implementations of this ADT, and we can test them as such without changing the client program at all.
This ADT leads to programs that are slightly less efficient than those in previous section for the connectivity application, because it does not take advantage of the property of that client that every union operation is immediately preceded by a find operation. We sometimes incur extra costs of this kind as the price of moving to a more abstract representation.
The combination of Program 1 through 3 is operationally equivalent to Program in previous section, but splitting the program into three parts is a more effective approach because it
- Separates the task of solving the high-level (connectivity) problem from the task of solving the low-level (union-find) problem, allowing us to work on the two problems independently
- Gives us a natural way to compare different algorithms and data structures for solving the problem
- Gives us an abstraction that we can use to build other algorithms
- Defines, through the interface, a way to check that the software is operating as expected
- Provides a mechanism that allows us to upgrade to new representations (new data structures or new algorithms) without changing the client program at all
These benefits are widely applicable to many tasks that we face when developing computer programs, so the basic tenets underlying ADTs are widely used.
2、FIFO Queues and Generalized Queues
The first-in, first-out (FIFO) queue is another fundamental ADT that is similar to the pushdown stack, but that uses the opposite rule to decide which element to remove for delete. Rather than removing the most recently inserted element, we remove the element that has been in the queue the longest.
Perhaps our busy professor’s “in” box should operate like a FIFO queue, since the first-in, first-out order seems to be an intuitively fair way to decide what to do next. However, that professor might not ever answer the phone or get to class on time! In a stack, a memorandum can get buried at the bottom, but emergencies are handled when they arise; in a FIFO queue, we work methodically through the tasks, but each has to wait its turn.
FIFO queues are abundant in everyday life. When we wait in line to see a movie or to buy groceries, we are being processed according to a FIFO discipline. Similarly, FIFO queues are frequently used within computer systems to hold tasks that are yet to be accomplished when we want to provide services on a first-come, first-served basis. Another example, which illustrates the distinction between stacks and FIFO queues, is a grocery store’s inventory of a perishable product. If the grocer puts new items on the front of the shelf and customers take items from the front, then we have a stack discipline, which is a problem for the grocer because items at the back of the shelf may stay there for a very long time and therefore spoil. By putting new items at the back of the shelf, the grocer ensures that the length of time any item has to stay on the shelf is limited by the length of time it takes customers to purchase the maximum number of items that fit on the shelf. This same basic principle applies to numerous similar situations.
Definition 1 A FIFO queue is an ADT that comprises two basic operations: insert (put) a new item, and delete (get) the item that was least recently inserted.
Program 4 FIFO queue ADT interface
This interface is identical to the pushdown stack interface, except for the names of the structure. The two ADTs differ only in the specification, which is not reflected in the code.

Program 4 is the interface for a FIFO queue ADT. This interface differs from the stack interface that we considered in previous section only in the nomenclature: to a compiler, say, the two interfaces are identical! This observation underscores the fact that the abstraction itself, which programmers normally do not define formally, is the essential component of an ADT. For large applications, which may involve scores of ADTs, the problem of defining them precisely is critical.
Figure 1 shows how a sample FIFO queue evolves through a series of get and put operations. Each get decreases the size of the queue by 1 and each put increases the size of the queue by 1. In the figure, the items in the queue are listed in the order that they are put on the queue, so that it is clear that the first item in the list is the one that is to be returned by the get operation. Again, in an implementation, we are free to organize the items any way that we want, as long as we maintain the illusion that the items are organized in this way.
 Figure 1 FIFO queue example
Figure 1 FIFO queue example
This list shows the result of the sequence of operations in the left column (top to bottom), where a letter denotes put and an asterisk denotes get. Each line displays the operation, the letter returned for get operations, and the contents of the queue in order from least recently inserted to most recently inserted, left to right.
To implement the FIFO queue ADT using a linked list, we keep the items in the list in order from least recently inserted to most recently inserted, as diagrammed in Figure 1. This order is the reverse of the order that we used for the stack implementation, but allows us to develop efficient implementations of the queue operations. We maintain two pointers into the list: one to the beginning (so that we can get first element), and one to the end (so that we can put a new element onto the queue), as shown in Figure 2 and in the implementation in Program 5.
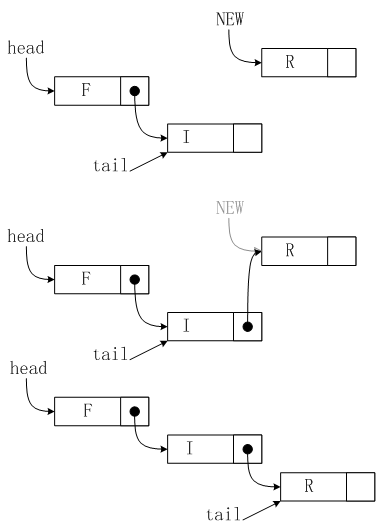 Figure 2 Linked-list queue
Figure 2 Linked-list queue
In this linked-list representation of a queue, we insert new items at the end, so the items in the linked list are in order from least recently inserted to most recently inserted, from beginning to end. The queue is represented by two pointers head and tail which point to the first and final item, respectively. To get an item from the queue, we remove the item at the front of the list, in the same way as we did for stacks. To put a new item onto the queue, we set the link field of the node referenced by tail to point to it (center), then update tail (bottom).
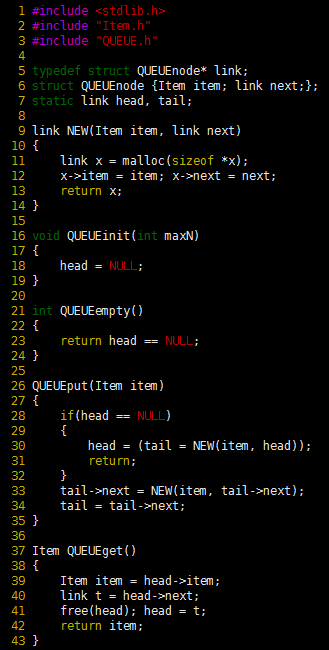 Program 5 FIFO queue linked-list implementation
Program 5 FIFO queue linked-list implementation
The difference between a FIFO queue and a pushdown stack is that new items are inserted at the end, rather than the beginning. Accordingly, this program keeps a pointer tail to the last node of the list, so that the function QUEUEput can add a new node by linking that node to the node referenced by tail and then updating tail to point to the new node. The functions QUEUEget, QUEUEinit, and QUEUEempty are all identical to their counterparts for the linked-list pushdown-stack implementation of the previous program.
We can also use an array to implement a FIFO queue, although we have to exercise care to keep the running time constant for both the put and get operations. That performance goal dictates that we can not move the elements of the queue within the array, unlike what might be suggested by a literal interpretation of Figure 1. Accordingly, as we did with the linked-list implementation, we maintain two indices into the array: one to the beginning of the queue and one to the end of the queue. We consider the contents of the queue to be the elements between the indices. To get an element, we remove it from the beginning (head) of the queue and increment the head index; to put an element, we add it to the end (tail) of the queue and increment the tail index. A sequence of put and get operations causes the queue to appear to move through the array, as illustrated in Figure 3. When it hits the end of the array, we arrange for it to wrap around to the beginning. The details of this computation are in the code in Program 6.
Property 1 We can implement the get and put operations for the FIFO queue ADT in constant time, using either arrays or linked list.
The fact is immediately clear when we inspect the code in Program 5 and Program 6.
Program 6 FIFO queue array implementation
The contents of the queue are all the elements in the array between head and tail, taking into account the wraparound back to 0 when the end of the array is encountered. If head and tail are equal, then we consider the queue to be empty; but if put would make them equal, then we consider it to be full. As usual, we do not check such error conditions, but we make the size of the array 1 greater than the maximum number of elements that the client expects to see in the queue, so that we could augment this program to make such checks.
 Figure 3 FIFO queue example, array implementation
Figure 3 FIFO queue example, array implementation
This sequence shows the data manipulation underlying the abstract representation in Figure 1 when we implement the queue by storing the items in an array, keeping indices to the beginning and end of the queue, and wrapping the indices back to the beginning of the array when they reach the end of the array. In this example, the tail index wraps back to the beginning when the second T is inserted, and the head index wraps when the second S is removed.
The same considerations that we discussed in previous section apply to space resources used by FIFO queues. The array representation requires that we reserve enough for the maximum number of items expected throughout the computation, whereas the linked-list representation uses space proportional to the number of elements in the data structure, at the cost of extra space for the links and extra time to allocate and deallocate memory for each operation.
Although we encounter stacks more often than we encounter FIFO queues, because of the fundamental relationship between stacks and recursive programs, we shall also encounter algorithms for which the queue is the natural underlying data structure. As we have already noted, one of the most frequent uses of queues and stacks in computational applications is to postpone computation. Although many applications that involve a queue of pending work operate correctly on matter what rule is used for delete, the overall running time or other resource usage may be dependent on the rule. When such applications involve a large number of insert and delete operations on data structures with a large number of items on them, performance differences are paramount. Accordingly, we devote a great deal of attention in this series to such ADTs. If we ignored performance, we could formulate a single ADT that encompassed insert and delete; since we do not ignore performance, each rule, in essence, constitutes a different ADT. To evaluate the effectiveness of a particular ADT, we need to consider two costs: the implementation cost, which depends on our choice of algorithm and data structure for the implementation; and the cost of the particular decision-making rule in terms of effect on the performance of the client.
Specifically, pushdown stacks and FIFO queues are special instances of a more general ADT: the generalized queue. Instances of generalized queues differ in only the rule used when items are removed. For stacks, the rule is “remove the item that was most recently inserted”; for FIFO queues, the rule is “remove the item that was least recently inserted”; and there are many other possibilities, a few of which we now consider.
A simple but powerful alternative is the random queue, where the rule is to “remove a random item,” and the client can expect to get any of the items on the queue with equal probability. We can implement the operations of a random queue in constant time using an array representation. As do stacks and FIFO queues, the array representation requires that we reserve space ahead of time. The linked-list alternative is less attractive that it was for stacks and FIFO queues, however, because implementing both insertion and deletion efficiently is a challenging task. We can use random queues as the basis for randomized algorithms, to avoid, with high probability, worst-case performance scenarios.
We have described stacks and FIFO queues by identifying items according to the time that they were inserted into the queue. Alternatively, we can describe these abstract concepts in terms of a sequential listing of the items in order, and refer to the basic operations of inserting and deleting items from the beginning and the end of the list. If we insert at the end and delete at the end, we get a stack (precisely as in our array implementation); if we insert at the beginning and delete at the beginning, we also get a stack (precisely as in our linked-list implementation); if we insert at the end and delete at the beginning, we get a FIFO queue (precisely as in our linked-list implementation); and if we insert at the beginning and delete at the end, we also get a FIFO queue (this option does not correspond to any of our implementations —— we could switch our array implementation to implement it precisely, but the linked-list implementation is not suitable because of the need to back up the pointer to the end when we remove the item at the end of the list). Building on this point of view, we are led to the deque ADT, where allow either insertion or deletion at either end.
Each of these ADTs also give rise to a number of related, but different, ADTs that suggest themselves as an outgrowth of careful examination of client programs and the performance of implementations.
3、Duplicate and Index Items
For many applications, the abstract items that we process are unique, a quality that leads us to consider modifying our idea of how stacks, FIFO queues, and other generalized ADTs should operate. Specifically, in this section, we consider the effect of changing the specifications of stacks, FIFO queues, and generalized queues to disallow duplicate items in the data structure.
For example, a company that maintains a mailing list of customers might want to try to grow the list by performing insert operations from other lists gathered from many sources, but would not want the list to grow for an insert operation that refers to a customer already on the list. We shall see that the same principle applies in a variety of applications. For another example, consider the problem of routing a message through a complex communications network. We might try going through several paths simultaneously in the network, but their is only one message, so any particular node in the network would want to have only one copy in its internal data structures.
One approach to handling this situation is to leave up to the clients the task of ensuring that duplicate items are not presented to the ADT, a task that clients presumably might carry out using some different ADT. But since the purpose of an ADT is to provide clients with clean solutions to applications problems, we might decide that detecting and resolving duplicates is a part of the problem that the ADT should help to solve.
The policy of disallowing duplicate items is a change in the abstraction: the interface, names of the operations, and so forth for such an ADT are the same as those for the corresponding ADT without the policy, but the behavior of the implementation changes in a fundamental way. In general, whenever we modify the specification of an ADT, we get a completely new ADT——one that has completely different properties. This situation also demonstrates the precarious nature of ADT specification: Being sure that clients and implementation adhere to the specifications in an interface is difficult enough, but enforcing a high-level policy such as this one is another matter entirely. Still, we are interested in algorithms that do so because clients can exploit such properties to solve problems in new ways, and implementations can take advantages of such restrictions to provide more efficient solutions.
Figure 4 shows how a modified no-duplicates stack ADT would operate for the example corresponding to previous Figure; Figure 5 shows the effect of the change for FIFO queues.
 Figure 4 Pushdown stack with no duplicates
Figure 4 Pushdown stack with no duplicates
This sequence shows the result of the result of the same operations as those in Figure 1 in previous section, but for a stack with no duplicate objects allowed. The gray squares mark situations where the stack is left unchanged because the item to be pushed is already on the stack. The number of items on the stack is limited by the number of possible distinct items.
 Figure 5 FIFO queue with no duplicates, ignore-the-new-item policy
Figure 5 FIFO queue with no duplicates, ignore-the-new-item policy
This sequence shows the result of the same operations as those in Figure 1 in this section, but for a queue with no duplicate objects allowed. The gray squares mark situations where the queue is left unchanged because the item to be put onto the queue is already there.
In general, we have a policy decision to make when a client makes an insert request for an item that is already in the data structure. Should we proceed as though the request never happened, or should we proceed as though the client had performed a delete followed by an insert? This decision affects the order in which items are ultimately processed for ADTs such as stacks and FIFO queues (see Figure 6), and the distinction is significant for client programs. For example, the company using such an ADT for a mailing list might prefer to use the new item (perhaps assuming that it has more up-to-date information about the customer), and the switching mechanism using such an ADT might prefer to ignore the new item (perhaps it has already taken steps to send along the message). Furthermore, this policy choice affects the implementations: the forget-the-old-item policy is generally more difficult to implement than the ignore-the-new-item policy, because it requires that we modify the data structure.
 Figure 6 FIFO queue with no duplicates, forget-the-old-item policy
Figure 6 FIFO queue with no duplicates, forget-the-old-item policy
This sequence shows the result of the same operations as in Figure 5, but using the (more difficult to implement) policy by which we always add a new item at the end of the queue. If there is a duplicate, we remove it.
There is an important special case for which we have a straight-forward solution, which is illustrated for the pushdown stack ADT in Program 7. This implementation assumes that the items are integers in the range 0 to M-1. Then, it uses a second array, indexed by the item itself, to determine whether that item is in the stack. When we insert item i, we set the ith entry in the array to 0. Otherwise, we use the same code as before to insert and delete items, with one additional test; Before inserting an item, we can test to see whether it is already in the stack. If it is, we ignore the push. This solution does not depend on whether we use an array or linked-list (or some other) representation for the stack. Implementing an ignore-the-old-item policy involves more work.
Program 7 Stack with index items and no duplicates
This pushdown-stack implementation assumes that all items are integers between 0 and maxN-1, so that it can maintain an array t that has a nonzero value corresponding to each item in the stack. The array enables STACKpush to test quickly whether its argument is already on the stack, and to take no action if the test succeeds. We use only the bit per entry in t, so we could save space by using characters or bits instead of integers, if desired.
In summary, one way to implement a stack with no duplicates using an ignore-the-new-item policy is to maintain two data structures: the first contains the items in the stack, as before, to keep track of the order in which the items in the stack were inserted; the second is an array that allows us to keep track of which items are in the stack, by using the item as an index. Using an array in this way is a special case of a symbol-table implementation, which is discussed later. We can apply the same technique to any generalized queue ADT, when we know the items to be integers in the range 0 to M-1.
This special case arises frequently. The most important example is when the items in the data structure are themselves array indices, so we refer to such items as index items. Typically, we have a set of M objects, kept in yet another array, that we need to pass through a generalized queue structure as a part of a more complex algorithm. Objects are put on the queue by index and processed when they are removed, and each object is to be processed precisely once. Using array indices in a queue with no duplicates accomplish this goal directly.
Each of these choices (disallow duplicates, or do not; and use the new item, or do not) leads to a new ADT. The differences may seem minor, but they obviously affect the dynamic behavior of the ADT as seen by client programs, and affect our choice of algorithm and data structure to implement the various operations, so we have no alternative but to treat all the ADTs as different. Furthermore, we have other options to consider: For example, we might wish to modify the interface to inform the client program when it attempts to insert a duplicate item, or to give the client the option whether to ignore the new item or to forget the old one.
When we informally use a term such as pushdown stack, FIFO queue, deque, priority queue, or symbol table, we are potentially refering to a family of ADTs, each with different sets of defined operations and different sets of conventions about the meanings of the operations, each requiring different and, in some cases, more sophisticated implementations to be able to support those operations efficiently.
