Our interfaces and implementations of stack and FIFO queue ADTs in Abstract Data Types～Stack ADT and Abstract Data Types～Queues and Unique Items provide clients with the capability to use a single instance of a particular generalized stack or queue, and to achieve the important objective of hiding from the client the particular data structure used in the implementation. Such ADTs are widely useful, and will serve as the basis for many of the implementations that we consider in this series.
1、First-Class ADTs
These objects mentioned above are disarmingly simple when considered as ADTs themselves, however, because there is only one object in a given program. The situation is analogous to having a program, for example, that manipulates only one integer. We could perhaps increment, decrement, and test the value of the integer, but could not declare variables or use it as an argument or return value in a function, or even multiply it by another integer. In this section, we consider how to construct ADTs that we can manipulate in the same way that we manipulate built-in types in client programs, while still achieving the objective of hiding the implementation from the client.
Definition 1 A first-class data type is one for which we can have potentially many different instances, and which we can assign to variables which we can declare to hold the instances.
For example, we could use first-class data types as arguments and return values to functions.
The method that we will use to implement first-class data types applies to any data type: in particular, it applies to generalized queues, so it provides us with the capability to write programs that manipulate stacks and FIFO queues in much the same way that we manipulate other types of data in C. This capability is important in the study of algorithms because it provides us with a natural way to express high-level operations involving such ADTs. For example, we can speak of operations to join two queues——to combine them into one. We shall consider algorithms that implement such operations for the priority queue ADT and for the symbol table ADT.
Some modern languages provide specific mechanisms. Being first-class ADTs, but the idea transcends specific mechanisms. Being able to manipulate instances of ADTs in much the same way that we manipulate built-in data types such as int or float is an important goal in the design of many high-level programming languages, because it allows any applications program to be written such that the program manipulates the objects of central concern to the application; it allows many programmers to work simultaneously on large systems, all using a precisely defined set of abstract operations; and it provides for those abstract operations to be implemented in many different ways without any changes to the applications code——for example for new machines and programming environments. Some languages even allow operator overloading, which allow us to use basic symbols such as + or * to define operators. C does not provide specific support for building first-class data types, but it does provide primitive operations that we can use to achieve that goal. There are a number of ways to proceed in C. To keep our focus on algorithms and data structures, as opposed to programming-language design issues, we do not consider all alternatives; rather, we describe and adopt just one convention that we can use throughout the series.
To illustrate the basic approach, we begin by considering, as an example, a first-class data type and then a first-class ADT for the complex-number abstraction. Our goal is to be able to write programs like Program 1, which performs algebraic operations on complex numbers using operations defined in the ADT. We implement the add and multiply operations as standard C functions, since C does not support operator overloading. Program 1 uses few properties of complex numbers; we now digress to consider these properties briefly. In one sense, we are not digressing at all, because it is interesting to contemplate the relationship between complex numbers themselves as a mathematical abstraction and this abstract representation of them in a computer program.
Program 1 Complex numbers driver (roots of unity)
This client program performs a computation on complex numbers using an ADT that allows it to compute directly with the abstraction of interest by declaring variables of type Complex and using them as arguments and return values of functions. This program checks the ADT implementation by computing the powers of the roots of unity. It prints the table shown in Figure 1.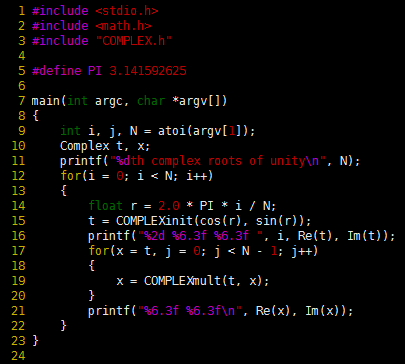
The number i = √-1 is an imaginary number. Although √-1 is meaningless as a real number, we name it i, and perform algebraic manipulations with i, replacing i² with -1 whenever it appears. A complex number consists of two parts, real and imaginary——complex numbers can be written in the form a + bi, where a and b are reals. To multiply complex numbers, we apply the usual algebraic rules, replacing i² with -1 whenever it appears. For example,
The real or imaginary parts might cancel out (have the value 0) when we perform a complex multiplication. For example,
Scaling the preceding equation by dividing through by
we find that
In general, there are many complex numbers that evaluate to 1 when raised to a power. These are the complex roots of unity. Indeed, for each N, there are exactly N complex numbers z with 
The numbers 
for k = 0, 1, …, N-1 are easily shown to have this property. For example, taking k = 1 and N = 8 in this formula gives the particular eighth root of unity that we just discovered. Program 1 is an example of a client program for the complex-numbers ADT that raises each of the Nth roots of unity of the Nth power, using the multiplication operation defined in the ADT. The output that it produces in shown in Figure 1: We expect that each number raised to the Nth power gives the same result: 1, or 1 + 0i.
Figure 1 Complex roots of unity
This table gives the output that is produced by Program 1 when invoked with ./complex 8. The eight complex roots of unity are ±1, ±i, and 
(left two columns). Each of these eight numbers gives the result 1 + 0i when raised to the eighth power (right two columns).
This client program differs from the client programs that we have considered to this point in one major respect: it declares variables of type Complex and assigns values to such variables, including using them as arguments and return values in functions. Accordingly, we need to define the type Complex in the interface.
Program 2 is an interface for complex numbers that we might consider using. It defines the type Complex as a struct comprising two floats (for the real and imaginary part of the complex number), and declares four functions for processing complex numbers: initialize, extract real and imaginary parts, and multiply. Program 3 gives implementations of these functions, which are straightforward. Together, these two functions provide an effective implementation of a complex-number ADT that we can use successfully in client programs such as Program 1.
The interface in Program 2 specifies one particular representation for complex number——a structure containing two integers (the real and imaginary parts). By including this representation within the interface, however, we are making it available for use by client programs. Programmers often organize interfaces in this way. Essentially, doing so amounts to publishing a standard representation for a new data type that might be used by many client programs. In this example, client programs could refer directly to t.Re and t.Im for any variable t of type Complex. The advantage of allowing such access is that we thus ensure that clients that need to directly implement their own manipulations that may not be present in the type’s suite of operations at least agree on the standard representation. The disadvantage of allowing clients direct access to the data is that we cannot change the representation without changing all the clients. In short, Program 2 is not an abstract data type, because the representation is not hidden by the interface.
Program 2 First-class data type for complex numbers
This interface for complex numbers includes a typedef that allows implementations to declare variables of type Complex and to use these variables as function arguments and return values. However, the data type is not abstract, because this representation is not hidden from clients.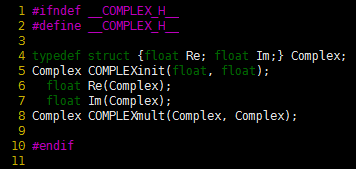
Program 3 Complex-numbers data-type implementation
These function implementations for the complex numbers data type are straightforward. However, we would prefer not to separate them from the definition of the Complex type, which is defined in the interface for the convenience of the client.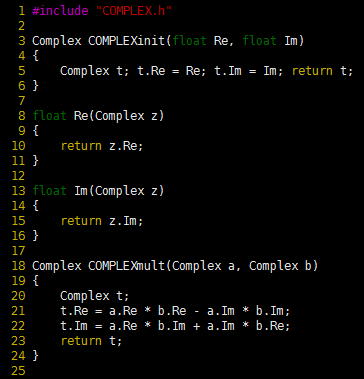
Even for this simple example, the difficulty of changing representations is significant because there is another standard representation that we might wish to consider using: polar coordinates. For an application with more complicated data structures, the ability to change representations is a requirement. For example, our company the needs to process mailing lists needs to use the same client program to process mailing lists in different formats. With a first-class ADT, the client programs can manipulate the data without direct access, but rather with indirect access, through operations defined in the ADT. An operation such as extract customer name then can have different implementations for different list formats. The most important implication of this arrangement is that we can change the data representation without having to change the client programs.’
We use the term handle to describe a reference to an abstract object. Our goal is to give client programs handles to abstract objects that can be used in assignment statements and as arguments and return values of functions in the same way as built-in data types, while hiding the representation of the objects from the client program.
Program 4 is an example of such an interface for complex numbers that achieves this goal, and exemplifies the conventions that we shall use throughout this series. The handle is defined as a pointer to a structure that has a name tag, but is otherwise not specified. The client can use this handle as intended, but there can be no code in the client program that uses the handle in any other way: It cannot access a field in a structure by dereferencing the pointer because it does not have the names of any of the fields. In the interface, we define functions which accept handles as arguments and also return handles as values; and client programs can use those functions, all without knowing anything about the data structure that will be used to implement the interface.
Program 5 is an implementation of the interface of Program 4. It defines the specific data structure that will be used to implement handles and the data type itself; a function that allocates the memory for a new object and initializes its field; functions that provide access to the fields (which we implement by dereferencing the handle pointer to access the specific fields in the argument objects); and functions that implement the ADT operations. ALL information specific to the data structure being used is guaranteed to be encapsulated in this implementation, because the client has no way to refer to it.
Program 4 First-class ADT for complex numbers
This interface provides clients with handles to complex number objects, but does not give any information about the representation——it is a struct that is not specified, except for its tag name.
Program 5 Complex-numbers ADT implementation
By contrast with Program 3, this implementation of the complex-numbers ADT includes the structure definition (which is hidden from the client), as well as the function implementations. Objects are pointers to structures, so we dereference the pointer to refer to the fields.
The distinction between the data type for complex numbers in the code in Program 2 and Program 3 and the ADT for complex numbers in the code in Program 4 and 5 is essential and is thus well worth careful study. It is a mechanism that we can use to develop and compare efficient algorithms for fundamental problems throughout this series. We shall not treat all the implications of using such a mechanism for software engineering in further detail, but it is a powerful and general mechanism that will serve us well in the study of algorithms and data structures and their application.
In particular, the issue of storage management is critical in the use of ADTs in software engineering. When we say x = t in Program 1, where the variables are both of type Complex, we simply are assigning a pointer. The alternative would be to allocate memory for a new object and define an explicit copy function to copy the values in the object associated with t to the new object. This issue of copy semantics is an important one to address in any ADT design. We normally use pointer assignment (and therefore do not consider copy implementations for our ADTs) because of our focus on efficiency—this choice makes us less susceptible to excessive hidden costs when performing operations on huge data structures. The design of the C string data type is based on similar considerations.
The implementation of COMPLEXmult in Program 3 creates a new object for the result. Alternatively, more in the spirit of reserving explicit object-creation operations for the client, we could return the value in one of the arguments. As it stands, COMPLEXmult has a defect called a memory leak, that makes the program unusable for a huge number of multiplications. The problem is that each multiplication allocates memory for a new object, but we never execute any calls to free. For this reason, ADTs often contain explicit destroy operations for use by clients. However, having the capability for destroy is no guarantee that clients will use it for each and every object created, and memory leaks are subtle defects that plague many large systems. For this reason, some programming environments have automatic mechanisms for the system to invoke destroy; other systems have automatic memory allocation, where the system takes responsibility to figure out which memory is no longer being used by programs, and to reclaim it. None of these solutions is entirely satisfactory. We rarely include destroy implementations in our ADTs, since these considerations are somewhat removed from the essential characteristics of our algorithms.
First-class ADTs play a central role in many of our implementations because they provide the necessary support for the abstract mechanisms for generic objects and collections of objects that we discussed in previous section. Accordingly, we use Item for the type of the items that we manipulate in the generalized queue ADTs in this series (and include an Item.h interface file), secure in the knowledge that an appropriate implementation will make our code useful for whatever data type a client program might need.
To illustrate further the general nature of the basic mechanism, we consider next a first-class ADT for FIFO queues using the same basic scheme that we just used for complex numbers. Program 6 is the interface for this ADT. It differs from Program in previous section in that it defines a queue handle (to be a pointer to an unspecified structure, in the standard manner) and each function takes a queue handle as an argument. With handles, client programs can manipulate multiple queues.
Program 7 is a driver program that exemplifies such a client. It randomly assigns N items to one of M FIFO queues, then prints out the contents of the queues, by removing the items one by one. Figure 2 is an example of the output produced by this program. Our interest in this program is to illustrate how the first-class data-type mechanism allows it to work with the queue ADT itself as a high-level object——it could easily be extended to test various methods of organizing queues to serve customers, and so forth.
Program 8 is an implementation of the FIFO queue ADT defined in Program 6, using linked lists for the underlying data structure. The primary difference between these implementations and these in Program in previous section has to do with the variables head and tail. In previous Program, we had only one queue, so we simply declared and used these variables in the implementation. In Program 8, each queue q has its own pointers head and tail, which we reference with the code q->head and q->tail. The definition of struct queue in an implementation answers the question “what is a queue?” for that implementation: In this case, the answer is that a queue is pointer to a structure consisting of the links to the head and tail of the queue. In an array implementation, a queue is a pointer to a struct consisting of a pointer to an array and two integers: the size of the array and the number of elements currently on the queue. In general, the members of the structure are exactly the global or static variable from the one-object implementation.
Program 6 First-class ADT interface for queues
We provide handles for queues in precisely the same manner as we did for complex numbers in Program 4: A handle is a pointer to a structure that is unspecified except for the tag name.
Program 7 Queue client program (queue simulation)
The availability of object handles makes it possible to build compound data structures with ADT objects, such as the array of queues in this sample client program, which simulates a situation where customers waiting for service are assigned at random to one of M service queues.
Figure 2 Random-queue simulation
This table gives the output that is produced when Program 7 is invoked with 84 as the command-line argument. The 10 queues have an average of 8.4 items each, ranging from a low of six to a high of 12.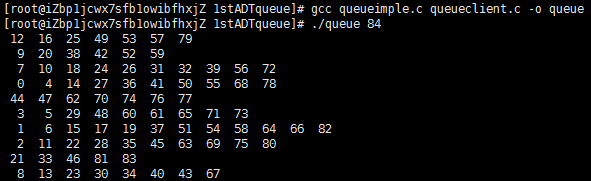
Program 8 Linked-list implementation of first-class queue
The code for implementations that provide object handles is typically more cumbersome than the corresponding code for single objects. This code does not check for errors such as a client attempt to get from an empty queue or an unsuccessful malloc.
With a carefully designed ADT, we can make use of the separation between client and implementations in many interesting ways. For example, we commonly use driver programs when developing or debugging ADT implementations. Similarly, we often use incomplete implementations of ADTs, called stubs, as placeholders while building systems to learn properties of clients, although this exercise can be tricky for clients that depend on the ADT implementation semantics.
As we saw in previous section, the ability to have multiple instances of a given ADT in a single program can lead us to complicated situations. Do we want to be able to have stacks or queues with different types of objects on them? How about different types of objects on the same queue? Do we want to use different implementations for queues of the same type in a single client because we know of performance differences? Should information about the efficiency of implementations be included in the interface? What form should that information take? Such questions underscore the importance of understanding the basic characteristics of our algorithms and data structures and how client programs may use them effectively, which is , in a sense, the topic of this series. Full implementations, however, are exercises in software engineering, rather than in algorithms design, so we stop short of developing ADTs of such generality in this series.
Despite its virtues, our mechanism for providing first-class ADTs comes at the (slight) cost of extra pointer dereferences and slightly more complicated implementation code, so we shall use the full mechanism for only those ADTs that require the use of handles as arguments or return values in interfaces. On the one hand, the use of first-class types might encompass the majority of the code in a small number of huge applications systems; on the other hand, an only-one-object arrangement-such as stacks, FIFO queues, and generalized queues of previous sections—and the use of typedef to specify the types of objects as described in previous section are quite serviceable techniques for many of the programs that we write.