As a final example in ADT series, we consider in this section an application-specific ADT that is representative of the relationship between applications domains and the algorithms and data structures of the type that we consider in this series.
1、Application-Based ADT example
The example that we shall consider is the polynomial ADT. It is drawn from symbolic mathematics, where we use the computer to help us manipulate abstract mathematical objects. Our goal is to be able to perform computations such as 
We also want to able to evaluate the polynomial for a given value of x. For x = 0.5, both sides of this equation have the value 1.1328125. The operations of multiplying, adding, and evaluating polynomials are at the heart of a great many mathematical calculations. Program 1 is a simple example that performs the symbolic operations corresponding to the polynomial equations
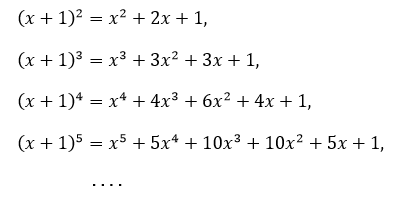The same basic ideas extend to include operations such as composition, integration, differentiation, knowledge of special functions, and so forth.
The first step is to define the polynomial ADT, as illustrated in the interface Program 2. For a well-understood mathematical abstraction such as a polynomial, the specification is so clear as to be unspoken (in the same way as for the ADT for complex numbers that we discussed in previous section): We want instances of the ADT to behave precisely in the same manner as the well-understood mathematical abstraction.
Program 1 Polynomial client (binomial coefficients)
This client program uses the polynomial ADT that is defined in the interface Program 2 to perform algebraic manipulations with polynomials. It takes an integer N and a floating-point number p from the command line, computes 
and checks the result by evaluating the resulting polynomial at x = p.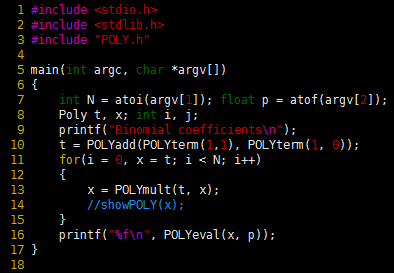
Program 2 First-class ADT interface for polynomicals
As usual, a handle to a polynomial is a pointer to a structure that is unspecified except for the tag name.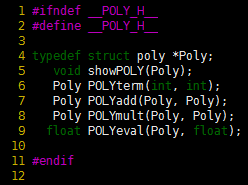
To implement the functions defined in the interface, we need to choose a particular data structure to represent polynomials and then to implement algorithms that manipulate the data structure to produce the behavior that client programs expect from the ADT. As usual, the choice of data structure affects the potential efficiency of the algorithms, and we are free to consider several. Also as usual, we have the choice of using a linked representation or an array representation. Program 3 is an implementation using an array representation.
To add two polynomials, we add their coefficients. If the polynomials are represented as arrays, the add functions amounts to a single loop through the arrays, as shown in Program 3. To multiply two polynomials, we use the elementary algorithm based on the distributive law. We multiply one polynomial by each term in the other, line up the results so that powers of x match, then add the terms to get the final result. The following table summarizes the computation for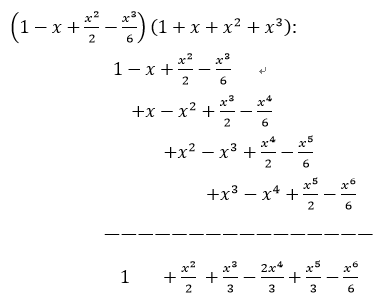 
The computation seems to require time proportional to N² to multiply two polynomials. Finding a faster algorithm for this task is a significant challenge. We shall consider this topic in detail in later series, where we shall see that it is possible to accomplish the task in time proportional to N³√N using a divide-and-conquer algorithm, and in time proportional to NlgN using the fast Fourier transform.
The implementation of the evaluate function in Program 3 uses a classic efficient algorithm known as Horner’s algorithm. A naive implementation of the function involves a direct computation using a function that computes
This approach take quadratic time. A less naive implementation involves saving the values of 
in a table, then using them in a direct computation. This approach takes linear extra space. Horner’s algorithm is a direct optimal linear algorithm based on parenthesizations such as 
Horner’s method is often presented as a time-saving trick, but it is actually an early and outstanding example of an elegant and efficient algorithm, which reduces the time required for this essential computational task from quadratic to linear. The calculation that we performed in previous program for converting ASCII strings to integers is a version of Horner’s algorithm.
Program 3 Array implementation of polynomial ADT
In this implementation of a first-class ADT for polynomials, a polynomial is a structure containing the degree and a pointer to an array of coefficients. For simplicity in this code, each addition operation modifies one of its arguments and each multiplication operation creates a new object. Another ADT operation to destroy objects (and to free the associated memory) might be needed for some applications.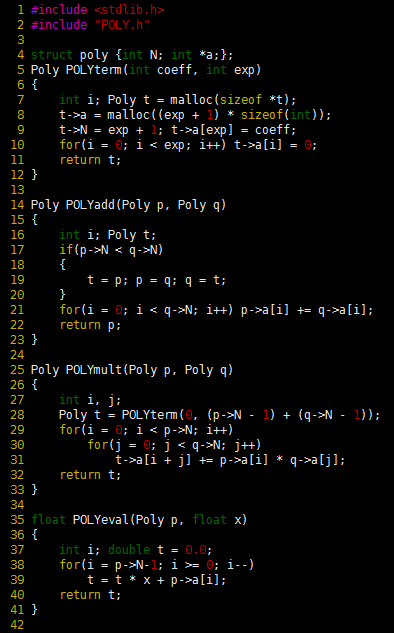
For simplicity and efficiency, POLYadd modifies one of its arguments; if we choose to use this implementation in an application, we should note that fact in the specification. Moreover, we have memory leaks, particularly in POLYmult, which creates a new polynomial to hold the result.
As usual, the array representation for implementing the polynomial ADT is but one possibility. If exponents are huge and there are not many terms, a linked-list representation might be more appropriate. For example, we would not want to use Program 3 to perfom a multiplication such as 
because it would use an array with space for hundreds of thousands of unused coefficients. We will explore the linked list option in more detail later.
2、Perspective
There are three primary reasons for us to be aware of the fundamental concepts underlying ADTs as we embark on the study of algorithms and data structures:
- ADTs are an important software-engineering tool in widespread use, and many of the algorithms that we study serve as implementations for fundamental ADTs that are widely applicable.
- ADTs help us to encapsulate the algorithms that we develop, so that we can use the same code for many different purposes.
- ADTs provide a convenient mechanism for our use in the process of developing and comparing the performance of algorithms.
Ideally, ADTs embody the common-sense principle that we are obligated to describe precisely the ways in which we manipulate our data. The client-interface-implementation mechanism that we have considered in detail in this series is convenient for this task in C, and provides us with C code that has a number of desirable properties. Many modern languages have specific support that allows the development of programs with similar properties, but the general approach transcends particular languages——when we do not have specific language support, we adopt programming conventions to maintain the separation that we would like to have among clients, interfaces, and implementations.
As we consider an ever-expanding set of choices in specifying the behavior of our ADTs, we are faced with an ever-expanding set of challenges in providing efficient implementations. The numerous examples that we have considered illustrate ways of meeting such challenges. We continually strive to achieve the goal of implementing all the operations efficiently, but we are unlikely to have a general-purpose implementation that can do so for all sets of operations. This situation works against the principles that lead us to ADTs in the first place, because in many cases implementors of ADTs need to know properties of client programs to know which implementations of associated ADTs will perform most efficiently, and implementors of client programs need to know performance properties of various implementations to know which to choose for a particular application. As ever, we must strike a balance. In this series, we consider numerous approaches to implementations for variants of fundamental ADTs, all of which have important applications.
We can use one ADT to build another. We have used the pointer and structure abstractions provided by C to build linked lists, then we have used linked lists or the array abstraction provided by C to build pushdown stacks, then we use pushdown stacks to get the capbility to evaluate arithmetic expressions. The ADT concept allows us to construct large systems on different layers of abstraction, from the machine-language instructions provided by the computer, to the various capabilities provided by the programming language, to sorting, searching and other higher-level capabilities provided by algorithms as discussed in previous series, to the even higher levels of abstraction that various applications require, as discussed later. ADTs are one point on the continuum of developing ever more powerful abstract mechanisms that is the essence of using computers effectively in problem solving.