Integrity constraints ensure that changes made to the database by authorized users do not result in a loss of data consistency. Thus, integrity constraints guard against accidental damage to the database. Examples of integrity constraints are:
- An instructor name cannot be null.
- No two instructors can have the same instructor ID.
- Every department name in the course relation must have a matching department name in the department relation.
- The budget of a department must be greater than $0.00.
1、Integrity Constraints
In general, an integrity constraint can be an arbitrary predicate pertaining to the database. However, arbitrary predicates may be costly to test. Thus, most database systems allow one to specify integrity constraints that can be tested with minimal overhead.
We have already seen some forms of integrity constraints in previous section. We study some more forms of integrity constraints in this section. We will study another form of integrity constraint, called functional dependencies, that is used primarily in the process of schema design later.
Integrity constraints are usually identified as part of the database schema design process, and declared as part of the create table command used to create relations. However, integrity constraints can also be added to an existing relation by using the command alter table table-name add constraint, where constraint can be any constraint on the relation. When such a command is executed, the system first ensures that the relation satisfies the specified constraint. If it does, the constraint is added to the relation; if not, the command is rejected.
1.1 Constraints on a Single Relation
We described in previous section how to define tables using the create table command. The create table command may also include integrity-constraint statements. In addition to the primary-key constraint, there are a number of other ones that can be included in the create table command. The allowed integrity constraints include
- not null
- unique
- check(<predicate>)
We cover each of these types of constraints in the following sections.
1.2 Not Null Constraint
As we discussed in previous section, the null value is a member of all domains, and as a result is a legal value for every attribute in SQL by default. For certain attributes, however, null values may be inappropriate. Consider a tuple in the student relation where name is null. Such a tuple gives student information for an unknown student; thus, it does not contain useful information. Similarly, we would not want the department budget to be null. In cases such as this, we wish to forbid null values, and we can do so by restricting the domain of the attributes name and budget to exclude null values, by declaring it as follows:
The not null specification prohibits the insertion of a null value for the attribute. Any database modification that would cause a null to be inserted in an attribute declared to be not null generates an error diagnostic.
There are many situations where we want to avoid null values. In particular, SQL prohibits null values in the primary key of a relation schema. Thus, in our university example, in the department relation, if the attribute dept_name is declared as the primary key for department, it cannot take a null value. As a result it would not need to be declared explicitly to be not null.
1.3 Unique Constraint
SQL also supports an integrity constraint:
The unique specification says that attributes Aj1, Aj2, . . . , Ajm form a candidate key; that is, no two tuples in the relation can be equal on all the listed attributes. However, candidate key attributes are permitted to be null unless they have explicitly been declared to be not null. Recall that a null value does not equal any other value.
1.4 The check Clause
When applied to a relation declaration, the clause check(P) specifies a predicate P that must be satisfied by every tuple in a relation. A common use of the check clause is to ensure that attribute values satisfy specified conditions, in effect creating a powerful type system. For instance, a clause check (budget > 0) in the create table command for relation department would ensure that the value of budget is nonnegative. As another example, consider the following:
Here, we use the check clause to simulate an enumerated type, by specifying that semester must be one of ‘Fall’, ‘Winter’, ‘Spring’, or ‘Summer’. Thus, the check clause permits attribute domains to be restricted in powerful ways that most programming-language type systems do not permit. The predicate in the check clause can, according to the SQL standard, be an arbitrary predicate that can include a subquery. However, currently none of the widely used database products allows the predicate to contain a subquery.
1.5 Referential Integrity
Often, we wish to ensure that a value that appears in one relation for a given set of attributes also appears for a certain set of attributes in another relation. This condition is called referential integrity.
Foreign keys can be specified as part of the SQL create table statement by using the foreign key clause, as we saw earlier. We illustrate foreign-key declarations by using the SQL DDL definition of part of our university database, show in Figure 1. The definition of the course table has a declaration “foreign key (dept_name) references department“. This foreign-key declaration specifies that for each course tuple, the department name specified in the tuple must exist in the department relation. Without this constraint, it is possible for a course to specify a nonexistent department name.
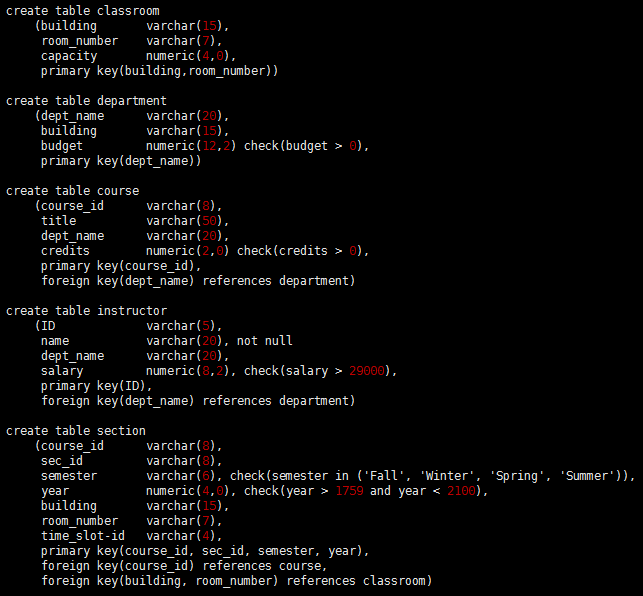Figure 1 SQL data definition for part of the university database.
More generally, let r1 and r2 be relations whose set of attributes are R1 and R2, respectively, with primary keys K1 and K2. We say that a subset α of R2 is a foreign key referencing K1 in relation r1 if it is required that, for every tuple t2 in r2, there must be a tuple t1 in r1 such that t1.K1 = t2.α.
Requirements of this form are called referential-integrity constraints, or subset dependencies. The latter term arises because the preceding referential-integrity constraint can be stated as a requirement that the set of values on α in r2 must be a subset of the values on K1 in r1. Note that, for a referential-integrity constraint to make sense, α and K1 must be compatible sets of attributes; that is, either α must be equal to K1, or they must contain the same number of attributes, and the types of corresponding attributes must be compatible (we assume here that α and K1 are ordered). Unlike foreign-key constraints, in general a referential integrity constraint does not require K1 to be a primary key of r1; as a result, more than one tuple in r1 can have the same value for attributes K1.
By default, in SQL a foreign key references the primary-key attributes of the referenced table. SQL also supports a version of the references clause where a list of attributes of the referenced relation can be specified explicitly. The specified list of attributes must, however, be declared as a candidate key of the referenced relation, using either a primary key constraint, or a unique constraint. A more general form of a referential-integrity constraint, where the referenced columns need not be a candidate key, cannot be directly specified in SQL.
We can use the following short form as part of an attribute definition to declare that the attribute forms a foreign key:
When a referential-integrity constraint is violated, the normal procedure is to reject the action that caused the violation (that is, the transaction performing the update action is rolled back). However, a foreign key clause can specify that if a delete or update action on the referenced relation violates the constraint, then, instead of rejecting the action, the system must take steps to change the tuple in the referencing relation to restore the constraint. Consider this definition of an integrity constraint on the relation course:
Because of the clause on delete cascade associated with the foreign-key declaration, if a delete of a tuple in department results in this referential-integrity constraint being violated, the system does not reject the delete. Instead, the delete “cascades” to the course relation, deleting the tuple that refers to the department that was deleted. Similarly, the system does not reject an update to a field referenced by the constraint if it violates the constraint; instead, the system updates the field dept_name in the referencing tuples in course to the new value as well. SQL also allows the foreign key clause to specify actions other than cascade, if the constraint is violated: The referencing field (here, dept_name) can be set to null (by using set null in place of cascade), or to the default value for the domain (by using set default).
If there is a chain of foreign-key dependencies across multiple relations, a deletion or update at one end of the chain can propagate across the entire chain. If a cascading update or delete causes a constraint violation that cannot be handled by a further cascading operation, the system aborts the transaction. As a result, all the changes caused by the transaction and its cascading actions are undone.
Null values complicate the semantics of referential-integrity constraints in SQL. Attributes of foreign keys are allowed to be null, provided that they have not otherwise been declared to be not null. If all the columns of a foreign key are nonnull in a given tuple, the usual definition of foreign-key constraint is used for that tuple. If any of the foreign-key columns is null, the tuple is defined automatically to satisfy the constraint. This definition may not always be the right choice, so SQL also provides constructs that allow you to change the behavior with null values; we do not discuss the constructs here.
1.6 Integrity Constraint Violation During a Transaction
Transactions may consist of several steps, and integrity constraints may be violated temporarily after one step, but a later step may remove the violation. For instance, suppose we have a relation person with primary key name, and an attribute spouse, and suppose that spouse is a foreign key on person. That is, the constraint says that the spouse attribute must contain a name that is present in the person table. Suppose we wish to note the fact that John and Mary are married to each other by inserting two tuples, one for John and one for Mary, in the above relation, with the spouse attributes set to Mary and John, respectively. The insertion of the first tuple would violate the foreign-key constraint, regardless of which of the two tuples is inserted first. After the second tuple is inserted the foreign-key constraint would hold again.
To handle such situations, the SQL standard allows a clause initially deferred to be added to a constraint specification; the constraint would then be checked at the end of a transaction, and not at intermediate steps. A constraint can alternatively be specified as deferrable, which means it is checked immediately by default, but can be deferred when desired. For constraints declared as deferrable, executing a statement set constraints constraint-list deferred as part of a transaction causes the checking of the specified constraints to be deferred to the end of that transaction.
However, you should be aware that the default behavior is to check constraints immediately, and many database implementations do not support deferred constraint checking. We can work around the problem in the above example in another way, if the spouse attribute can be set to null: We set the spouse attributes to null when inserting the tuples for John and Mary, and we update them later. However, this technique requires more programming effort, and does not work if the attributes cannot be set to null.
1.7 Complex Check Conditions and Assertions
The SQL standard supports additional constructs for specifying integrity constraints that are described in this section. However, you should be aware that these constructs are not currently supposed by most database systems. As defined by the SQL standard, the predicate in the check clause can be an arbitrary predicate, which can include a subquery. If a database implementation supports subqueries in the check clause, we could specify the following referential-integrity constraint on the relation section:
The check condition verifies that the time_slot_id in each tuple in the section relation is actually the identifier of a time slot in the time_slot relation. Thus, the condition has to be checked not only when a tuple is inserted or modified in section, but also when the relation time_slot changes (in this case, when a tuple is deleted or modified in relation time_slot).
Another natural constraint on our university schema would be to require that every section has at least one instructor teaching the section. In an attempt to enforce this, we may try to declare that the attributes (course_id, sec_id, semester, year) of the section relation form a foreign key referencing the corresponding attributes of the teaches relation. Unfortunately, these attributes do not form a candidate key of the relation teaches. A check constraint similar to that for the time_slot attribute can be used to enforce this constraint, if check constraints with subqueries were supported by a database system.
Complex check conditions can be useful when we want to ensure integrity of data, but may be costly to test. For example, the predicate in the check clause would not only have to be evaluated when a modification is made to the section relation, but may have to be checked if a modification is made to the time_slot relation because that relation is referenced in the subquery.
An assertion is a predicate expressing a condition that we wish the database always to satisfy. Domain constraints and referential-integrity constraints are special forms of assertions. We have paid substantial attention to these forms of assertions because they are easily tested and apply to a wide range of database applications. However, there are many constraints that we cannot express by using only these special forms. Two examples of such constraints are:
- For each tuple in the student relation, the value of the attribute tot_cred must equal the sum of credits of courses that the student has completed successfully.
- An instructor cannot teach in two different classrooms in a semester in the same time slot.
An assertion in SQL takes the form:
In Figure 2, we show how the first example of constraints can be written in SQL. Since SQL does not provide a “for all X, P(X)” construct (where P is a predicate), we are forced to implement the constraint by an equivalent construct, “not exists X such that not P(X)“, that can be expressed in SQL.
Figure 2 An assertion example.
When an assertion is created, the system tests it for validity. If the assertion is valid, then any future modification to the database is allowed only if it does not cause that assertion to be violated. This testing may introduce a significant amount of overhead if complex assertions have been made. Hence, assertions should be used with great care. The high overhead of testing and maintaining assertions has led some system developers to omit support for general assertions, or to provide specialized forms of assertion that are easier to test.
Currently, none of the widely used database systems supports either subqueries in the check clause predicate, or the create assertion construct. However, equivalent functionality can be implemented using triggers, which are described later, if they are supported by database system.