For our final example of a recursive program in this series, we consider one of the most important of all recursive programs: recursive graph traversal, or depth-first search. This method for systematically visiting all the nodes in a graph is a direct generalization of the tree-traversal methods that we considered in Recursion and Trees~ Mathematical Properties of Trees and Tree Traversal, and it serves as the basis for many basic algorithms for processing graph.
1、Graph Traversal
It is a simple recursive algorithm. Starting at any node v, we
- Visit v.
- (Recursively) visit each (unvisited) node attached to v.
If the graph is connected, we eventually reach all of the nodes. Program 1 is an implementation of this recursive procedure.
For example, suppose that we use the adjacency-list representation depicted in the sample graph in Figure 5 in Elementary Data Structures ~ Compound Data Structures. Figure 1 shows the recursive calls made during the depth-first search of this graph, and the sequence on the left in Figure 2 depicts the way in which we follow the edges in the graph. We follow each edge in the graph, with one of two possible outcomes: if the edge takes us to a node that we have already visited, we ignore it; if it takes us to a node that we have not yet visited, we follow it there via a recursive call. The set of all edges that we follow in this way forms a spanning tree for the graph.
The difference between depth-first search and general tree traversal (see Program 1 in Recursion and Trees~ Mathematical Properties of Trees and Tree Traversal) is that we need to guard explicitly against visiting nodes that we have already visited. In a tree, we never encounter any such nodes. Indeed, if the graph is a tree, recursive depth-first search starting at the root is equivalent to preorder traversal.
Program 1 Depth-first search
To visit all the nodes connected to node k in a graph, we mark it as visited, then (recursively) visit all the unvisited nodes on k‘s adjacency list. Figure 1 Depth-first-search function calls
Figure 1 Depth-first-search function calls
This sequence of function calls constitutes depth-first search for the example graph in Figure 5 in Elementary Data Structures ~ Compound Data Structures. The tree that depicts the recursive-call structure (top) is called the depth-first-search tree.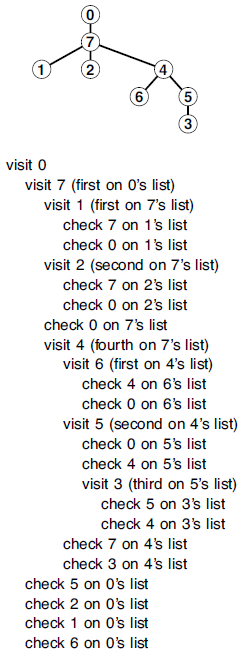
Figure 2 Depth-first search and breadth-first search
Depth-first search (left) moves from node to node, backing up to the previous node to try the next possibility whenever it has tried every possibility at a given node. Breadth-first search (right) exhausts all the possibilities at one node before moving to the next.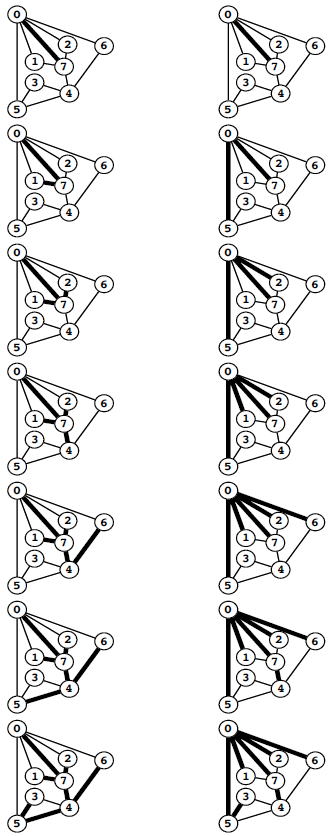
Property 1 Depth-first search requires time proportional to V + E in a graph with V vertices and E edges, using the adjacency lists representation.
In the adjacency lists representation, there is one list node corresponding to each edge in the graph, and one list head pointer corresponding to each vertex in the graph. Depth-first search touches all of them, at more once.
Because it also takes time proportional to V + E to build the adjacency lists representation from an input sequence of edges (see Program 5 in Elementary Data Structures ~ Compound Data Structures), depth-first search gives us a linear-time solution to the connectivity program of Introduction series. For huge graphs, however, the union-find solutions might still be preferable, because representing the whole graph takes space proportional to E, while the union-find solutions take space only proportional to V.
As we did with tree traversal, we can define a graph-traversal method that uses an explicit stack, as depicted in Figure 3. We can think of an abstract stack that holds dual entries: a node and a pointer into that node’s adjacency list. With the stack initialized to the start node and a pointer initialized to the first node on that node’s adjacency list, the depth-first search algorithm is equivalent to entering into a loop, where we visit the node at the top of the stack (if it has not already been visited); save the node referenced by the current adjacency-list pointer; update the adjacency list reference to the next node (popping the entry if at the end of the adjacency list); and push a stack entry for the saved node, referencing the first node on its adjacency list.
Alternatively, as we did for tree traversal, we can consider the stack to contain links to nodes only. With the stack initialized to the start node, we enter into a loop where we visit the node at the top of the stack (if it has not already been visited), then push all the nodes adjacent to it onto the stack. Figure 3 illustrates that both of these methods are equivalent to depth-first search for our example graph, and the equivalence indeed holds in general.
Figure 3 Depth-first-search stack dynamics
We can think of the pushdown stack supporting depth-first search as containing a node and a reference to that node’s adjacency list (indicated by a circled node) (left). Thus, we begin with node 0 on the stack, with reference to the first node on its list, node 7. Each line indicates the result of popping the stack, pushing a reference to the next node on the list for nodes that have been visited, and pushing an entry on the stack for nodes that have not been visited. Alternatively, we can think of the process as simply pushing all nodes adjacent to any unvisited node onto the stack (right).
The visit-the-top-node-and-push-all-its-neighbors algorithms is a simple formulation of depth-first search, but it is clear from Figure 3 that is suffers the disadvantage of possibly leaving multiple copies of each node on the stack. It does so even if we test whether each node that is about to go on the stack has been visited and refrain from putting the node in the stack if it has been. To avoid this problem, we can use a stack implementation that disallows duplicates by using a forget-the-old-item policy, because the copy nearest the top of the stack is always the first one visited, so the others are simply popped.
The stack dynamics for depth-first search that are illustrated in Figure 3 depend on the nodes on each adjacency list ending up on the stack in the same order that they appear in the list. To get this ordering for a given adjacency list when pushing one node at a time, we would have to push the last node first, then the next-to-last node, and so forth. Moreover, to limit the stack size to the number of vertices while at the same time visiting the nodes in the same order as in depth-first search, we need to use a stack discipline with a forget-the-old-item policy. If visiting the nodes in the same order as depth-first search is not important to us, we can avoid both of these complications and directly formulate a nonrecursive stack-based graph-traversal method: With the stack initialized to the start node, we enter into a loop where we visit the node at the top of the stack, then proceed through its adjacency list, pushing each node onto the stack (if the node has not been visited already), using a stack implementation that disallows duplicates with an ignore-the-new-item policy. This algorithm visits all the nodes in the graph in a manner similar to depth-first-search, but it is not recursive.
The algorithm in the previous paragraph is noteworthy because we could use any generalized queue ADT, and still visit each of the nodes in the graph (and generate a spanning tree). For example, if we use a queue instead of a stack, then we have breadth-first search, which is analogous to level-order traversal in a tree. Program 2 is an implementation of this method (assuming that we use a queue implementation like Program 7 in Abstract Data Types~Queues and Unique Items); an example of the algorithm in operation is depicted in Figure 4. In later part, we shall examine numerous graph algorithms based on more sophisticated generalized queue ADTs.
Breadth-first search and depth-first search both visit all the nodes in a graph, but their manner of doing so is dramatically different, as illustrated in Figure 5. Breadth-first search amounts to an army of searchers fanning out to cover the territory; depth-first search corresponds to a single searcher probing unknown territory as deeply as possible, retreating only when hitting dead ends. These are basic problem-solving paradigms of significance in many areas of computer science beyond graph searching.
Figure 4 Breadth-first-search queue dynamics
We start with 0 on the queue, then get 0, visit it, and put then nodes on its adjacency list 7 5 2 1 6, in that order onto the queue. Then we get 7, visit it, and put the nodes on its adjacency list, and so forth. With duplicates disallowed with an ignore-the-new-item policy (right), we get the same result without any extraneous queue entries.
Figure 5 Graph-traversal trees
This diagram shows depth-first search (center) and breadth-first search (bottom), halfway through searching in a large graph (top). Depth-first search meanders from one node to the next, so most nodes are connected to just two others. By contrast, breadth-first search sweeps through the graph, visiting all the nodes connected to a given node before moving on, so several nodes are connected to many others.
2、Perspective
Recursion lies at the heart of early theoretical studies into the nature of computation. Recursive functions and programs play a central role in mathematical studies that attempt to separate problems that can be solved by a computer from problems that cannot be.
It is certainly impossible to do justice to topics as far-reaching as trees and recursion in so brief a discussion. Many of the best examples of recursive programs will be our focus throughout the series——divide-and-conquer algorithms and recursive data structures that have been applied successfully to solve a wide variety of problems. For many applications, there is no reason to go beyond a simple, direct recursive implementation; for others, we will consider the derivation of alternate nonrecursive and bottom-up implementations.
In these series, our interest lies in the practical aspects of recursive programs and data structures. Our goal is to exploit recursion to produce elegant and efficient implementations. To meet that goal, we need to have particular respect for the dangers of simple programs that lead to an exponential number of function calls or impossibly deep nesting. Despite this pitfall, recursive programs and data structures are attractive because they often provide us with inductive arguments that can convince us that our programs are correct and efficient.
We use trees throughout these series, both to help us understand the dynamic properties of programs, and as dynamic data structures. Despite its central role in algorithm design, recursion is not a panacea. As we discovered in our study of tree- and graph-traversal algorithms, stack-based (inherently recursive) algorithms are not the only option when we have multiple computational tasks to manage. An effective algorithm-design technique for many problems is the use of generalized queue implementations other than stacks to give us the freedom to choose the next task according to some more subjective criteria than simply choosing the most recent.
