The primary quantities of interest in EMC problems are conducted emissions [voltage in volts (V), and current in amperes (A)] and radiated emissions [electric field in volts per meter (V/m) and magnetic field in amperes per meter (A/m)]. Associated with these primary quantities are the quantities of power in watts (W) or power density in watts per square meter (W/m²). The numerical range of these quantities can be quite large.For example, electric fields can have values ranging from 1μV/m to 200 V/m. This represents a dynamic range of over eight orders of magnitude (10²×10²×10²×10²). Because these wide ranges in units are common in the ECM community, EMC units are expressed in decibels (dB). Decibels have the property of compressing data, e.g., a range of voltage of 10²×10²×10²×10² is 160 dB.
The ear tends to hear logarithmically so describing the effect of noise in dB is natural. To begin with discussion, consider the amplifier circuit shown in Fig. 1. A source consisting of an open-circuit voltage Vs and source resistance Rs delivers a signal to an amplifier whose load is represented by Rl. The input resistance to the amplifier is denoted by Rin and the power delivered to the amplifier is 
where the input voltage is expressed as RMS (root-mean-squared) and differs from the peak value of the sinusoidal voltage, vpeak, by vRMS = vpeak / √2.
Figure 1 An illustration of the definition and use of the decibel (dB).
There are two common ways of expressing values of voltages and currents: peak and RMS. If we write the equation of a sinusoidal voltage as V sin(ωt) the maximum or peak value of the wave is V. If this voltage is applied across a resistor R the average power delivered to the resistor is Pav = (1/2)(V²/R)watts. On the other hand it is common in industry to express sinusoidal voltage and currents as RMS where Vrms = V / √2 and V is the peak value of the waveform. In this case the average power delivered to a resistor is Pav = Vrms² / R watts and no 1/2 factor is required. This is the only consequence of expressing sinusoidal voltages and currents in peak or RMS. For example, household voltages in the U.S. are 120 volts (RMS) which is 170 volts (peak). Test and measurement equipment are almost universally calibrated in RMS and not peak.
The power delivered to the load is 
The power gain of the amplifier is 
The power gain expressed in decibels is defined as 
where log10 is the logarithm to the base 10. The related quantities of interest are the voltage gain and current gain of the amplifier. These are defined by 
In dB these are defined as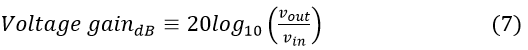 
Note that power gain in dB is defined as 10log10 of the ratio of the two quantities, whereas voltage gain and current gain in dB are defined as 20log10 of the ratio of the two quantities! Although this could be taken as simply definition, there is a rationale for it. To see this, observe that if the input resistance to the amplifier equals the load resistance, Rl = Rin, then (3) becomes
In dB the power gain becomes, for Rin = Rl
from which we obtain the defining relation for expression the voltage gain in dB as in (7). In summary, the ratio of two quantities in dB is given by
1、Power Loss in Cables
Computing the power loss in long connection cables is another example that illustrates the utility of expressing quantities in dB. To begin that discussion, we need to briefly review the topic of transmission lines. Consider the transmission line of length L shown in Fig. 2. The line is usually characterized in terms of its characteristic impedance ^ZC and velocity of propagation of waves on the line v. Although we may be interested in the behavior of the line when arbitrary time-domain pulses are applied to it, we are usually concerned with its sinusoidal steady-state behavior, i.e., for single frequency, sinusoidal excitation after all transients have died out.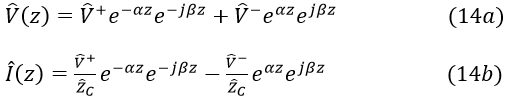 
For sinusoidal steady-state excitation of systems, the reader should review the phasor solution method discussed later.