前文 信号完整性小记 ~ 时域与频域 已对时域与频域分析方法进行了相关阐述，本文对电容与电感的电气模型和物理基础进行论述，以便在实际使用中根据设计需求确定具体参数，达到预期效果。
1、阻抗与电气模型
1.1 时域中的容抗
电容的容抗可以用上式表示，它表示电容器的容抗与电容值以及两端的电压波形相关。如果电压波形的斜率很大（电压变化较快），则流过的电流很大，电容器的容抗很小。在电压信号的变化率相同时，电容器的电容值越大，它的容抗就越小。
1.2 时域中的感抗
时域中的感抗表达式如上式所示，感抗与电感值成正比。如果流过电感器的电流突变，感抗就很大。直流电流时电感器的感抗近似为零。然而，电感器的实际阻抗与电流的确切波形有及其密切的关系。
2、电容的物理基础
2.1 电容的静态定义
电容的静态定义为下式：
Figure 1 Capacitance is a measure of the capacity to store charge for a given voltage between the conductors.
两平行板间距为 h, 面积为 A, 电容量为下式所示。如果介质不是空气，在前面再乘以一个系数。
2.2 电容的去耦能力
流经电容的动态电流与其上动态电压之间的关系见下式。由于电容器的能量CV²/2
不能突变，故成就了电容电压不突变的去耦效果。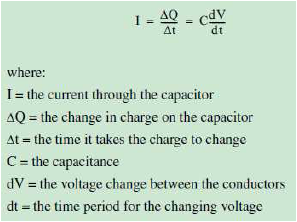
为了芯片的稳压，常在负载芯片附近加去耦电容，在时间 δt 内，电容器 C 阻止电压 V 下降（实际是电容想芯片供电）。假设芯片功耗为 P，电压下降 5% 的去耦时间 δt 近似为：
式中 V²/P=V/I=R（负载阻抗），故上式即为 δt = 0.05RC。可知，电容器放电持续到时间常数 RC 的5%时，电压降下降到原值的 95%。
3、电感的物理基础
3.1 电感的静态定义
在信号完整性分析中，电感降压，电容稳压，电感与电容之间是你死我活的斗争。电感对信号完整性的四类问题都有最严重的影响：电感性突变引起反射、线间感性耦合引起串扰、PDN（Power Distributed Network）中的电感引起轨道塌陷及 EMI。
电流的周围形成闭合磁力线圈 N，一段直导线，当有电流从中间流过时，在导线的周围将产生环形磁力线圈。距离电流越远，磁力线圈就越少，如果距离电流足够远，则磁力线圈将接近为零。可以用右手定则判定磁力线圈的方向。
电感的静态定义是当流过 1 安培电流时，周围磁力线器的韦伯值（Weber）N。
实际电感值只与导体的几何结构和材料的导磁率有关。
3.2 自感和互感
两条临近的导线 a 和 b, 如果只有一条导线 a 中有电流，在 a 的周围将会出现自磁力线圈，而其中的一部分也环绕了 b。导线自身电流产生的磁力线称为自磁力线圈，由临近导线产生的磁力线称为互磁力线圈。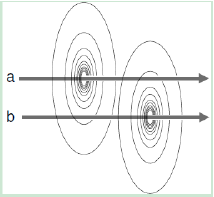
如果两导线中的电流方向相同，磁力线方向也就相同。导线 a 周围的磁力线圈净匝数等于自磁力线匝数加上互磁力线匝数。如果两导线中的电流方向相反，磁力线方向也就相反。导线 a 周围的磁力线圈净匝数等于自磁力线匝数减去互磁力线匝数，故匝数值减少了。
互感是一条导线中流过单位安培电流时，所产生的环绕在另一条导线周围的磁力线匝数。两条导线拉近时互感增大，反之则会减小。互感具有对称性，a 对 b 的互感等于 b 对 a 的互感。互感小于两个导体中任意一个的自感，即互感小于两导线自感的最小值。
3.3 电感的动态定义
只要一段导线周围的磁力线净匝数发生变化，导线两端就会感应出一个感应电压，该电压与磁力线匝数变化的快慢有关。导线周围的磁力线匝数为 N = LI，感应电压 V 与导线电感 L 和导线中电流变化率有关，如下式：
此公式也可看成是电感的动态定义，判断电感两端电压极性的准则是感应电压形成的感应电流将力图阻碍原电流的变化。
形成感应电压是电感在信号完整性中地位重大的原因，正是这个感应电压将引起反射、串扰、SSN（Simultaneous Switch Noise）噪声、轨道塌陷、地弹和大多数电磁干扰源（EMI）。
由于互感在导线 b 中的电流变化，在第一条导线 a 的两端将产生感应电压。人们用串扰去描述导线 a 上产生的感应电压噪声，其值为：
3.4 支路净电感及地弹
为了便于分析，提出了局部自感和局部互感的概念。实际中电流只在完整的回路中流动，我们强行假设除了所关心的那段导线外，其余处没有电流，由于仅考虑了电流回路的一部分，把这种电感称为局部自感。局部电流并不存在，因为必须要有电流回路。但由于整个回路的多样性和差异性，采用局部自感对分析、理解和计算电感很有用。局部自感的一个重要特征是电流分布越分散，局部自感越小。反之，电流分布密度越大，局部自感则越大，笼统地说，导线越细电感越大。两导线局部互感是各自局部自感的一小部分，若间距拉大，互感迅速减小。
如下图所示的两段导线组成一个完整的回路，如 IC 封装中的相邻信号引脚和返回引脚，在电路板上也可能是相邻信号平面和返回平面。
Figure 2 A current loop with two legs: an initial current and its return current.
电路中的两个支路都有其相应的局部自感 La 和 Lb，这两条电路间具有互感 Lab。回路中的电流 I 在支路 a、b 中大小相等，流向相反。在导线 b 的周围自身电流产生的磁力线匝数为 Nb = I × Lb，同时，在支路 b 的周围还有一些磁力线圈是源自于支路 a 的，匝数为 Nab = I × Lab。由于 a，b 中电流方向相反，于是支路 b 周围的磁力线净匝数为：
返回路径上的电压将为
如果支路 b 是返回路径，则路径 b 上产生的电压称为地弹。从上式可知，为了减少地弹，有两条途径：
- 尽可能减小回路电流的变化率；
- 尽可能减小局部自感 Lb，同时增大局部互感 Lab。
减少返回路径的局部自感，需要令返回路径短而宽，这就是使用地平面的原因。增大返回路径和初始路径间互感，两者需要尽量靠近。
当电流方向相同时，互磁力线圈和自磁力线圈方向相同，两者叠加，其中一条电源导线的净电感为 Lnet = La + Lb，此时为了减少电源引线的净电感，不仅要减少局部自感，还必须要减少引线之间的局部互感。
在设计电源分配网络时，减少支路净电感的设计规则是尽可能让同向平行电流之间的中心间距大于他们的长度，芯片的各个电源引线之间一定要远离！！！！！
Figure 3 Total inductance of one 100-mil-long wire bond when an adjacent wire bond carries the same current, for the two cases of the currents in the same direction and in opposite directions. The wires are pulled apart, comparing the total inductances with the partial self- and mutual inductances.
3.5 回路总电感
实际上，电流总是在完整的回路中流动，该完整电流回路的总电感称为回路电感。回路电感是当回路中流过单位安培电流时，环绕在整个回路周围的磁力线匝数。对于上面提到的电路，支路 a 可对应信号路径，支路 b 对应返回路径。整个回路的自感为：
当两支路靠得越近时，互感增大，局部自感保持不变，此时，回路的总电感就越小。一般来说，回路中两个支路的总电流方向总是相反，两条支路靠得越近，局部互感越大，回路的总电感越小。故减小回路电感的出发点是：使返回路径靠近信号路径，以增大两路径间的局部互感。电源与地平面要尽量靠近，以减少平面的回路电感，进而减少轨道塌陷和EMI。
两个相互独立的电流回路之间也会产生互感，如果磁力线匝数改变，还会产生噪声电压，噪声值为：
减少串扰开关噪声的方法是减少两个信号路径 — 返回路径回路间的互感：
- 通过拉大两回路间距实现。
- 由于互感小于两回路自感的最小值，减少两回路自感也可以减小回路间的互感。