The development of a string data type implementation similar to Program 5 and 6 is of particular interest, because character strings are widely used as sort keys.1、Index and Pointer Sorting
Using the C library string-comparison function, we can change the first three lines in Program 5 to
to convert it to an interface for strings. The implementation is more challenging than Program 6 in Sorting～Elementary Sorting Methods II because, when working with strings in C, we must be aware of the allocation of memory for the strings. Program 1 uses the method that we examined in Program 2 in Elementary Data Structures ~ Compound Data Structures, maintaining a buffer in the data-type implementation. Other options are to allocate memory dynamically for each string, or to keep the buffer in the client program. We can use this code (along with the interface described in the previous article) to sort strings of characters, using any of the sort implementations that we have been considering. Because strings are represented as pointers to arrays of characters in C, this program is an example of a pointer sort, which we shall consider shortly.
Program 1 Data-type implementation for string items
This implementation allows us to use our sorting programs to sort strings. A string is a pointer to a character, so a sort will process an array of pointers to characters, rearranging them so the indicated strings are in alphanumeric order. We statically allocate the storage buffer containing the string characters in this module; dynamic allocation is perhaps more appropriate. The ITEMrand implementation is omitted.
We are faced with memory-management choices of this kind any time that we modularize a program. Who should be responsible for managing the memory corresponding to the concrete realization of some type of object: the client, the data-type implementation, or the system? There is no hard-and-fast answer to this question (some programming-language designers become evangelical when the question is raised). Some modern programming systems (not C) have general mechanisms for dealing with memory management automatically. We will revisit this issue in later series.
One simple approach for sorting without (intermediate) moves of items is to maintain an index array with keys in the items accessed only for comparisons. Suppose that the items to be sorted are in an array data[0], . . . , data[N-1], and that we do not wish to move them around, for some reason (perhaps they are huge). To get the effect of sorting, we use a second array a of item indices. We begin by initializing a[ i ] to i for i = 0, . . . , N – 1. That is, we begin with a[0] having the index of the first data item, a[ 1 ] having the index of the second data item, and so on. The goal of the sort is to rearrange the index array a such that a[0] gives the index of the data item with the smallest key, a[ 1 ] gives the index of the data item with the second smallest key, and so on. Then we can achieve the effect of sorting by accessing the keys through the indices——for example, we could print out the array in sorted order in this way.
Now, we take advantage of the fact that our sort routines access data only through less and exch. In the item-type interface definition, we specify the type of the items to be sorted to be integers (in indices in a) with typedef int Item; and leave the exchange as before, but we change less to refer to the data through the indices:
For simplicity, this discussion assumes that the data are keys, rather than full items. We can use the same principle for larger, more complicated items, by modifying less to access specific keys in the items. The sort routines rearrange the indices in a , which carry the information that we need to access the keys. An example of this arrangements, with the same items sorted by two different keys, is shown in Figure 1.
Figure 1 Index sorting example
By manipulating indices, rather than the records themselves, we can sort an array simultaneously on several keys. For this sample data that might represent students’ names and grades, the second column is the result of an index sort on the name, and the third column is the result of an index sort on the grade. For example, Wilson is last in alphabetic order and has the tenth highest grade, while Adams is first in alphabetic order and has the sixth highest grade.
A rearrangement of the N distinct nonnegative integers less than N is called a permutation in mathematics: an index sort computes a permutation. In mathematics, permutations are normally defined as rearrangements of the integer 1 through N; we shall use 0 through N – 1 to emphasize the direct relationship between permutations and C array indices.
This index-array approach to indirection will work in any programming language that supports arrays. Another possibility, especially attractive in C, is to use pointers. For example, defining the data type
and then initializing a with
and doing comparisons indirectly with
is equivalent to using the strategy described in the preceding paragraph. This arrangement is known as a pointer sort. The string data-type implementation that we just considered (Program 1) is an example of a pointer sort. For sorting an array of fixed-size items, a pointer sort is essentially equivalent to an index sort, but with the address of the array added to each index. But a pointer sort is much more general, because the pointers could point anywhere, and the items being sorted do not need to be fixed in size. As is true in index sorting, if a is an array of pointers to keys, then a call to sort will result in the pointers being rearranged such that accessing them sequentially will access the keys in order. We implement comparisons by following pointers; we implement exchanges by exchanging the pointers.
The standard C library sort function qsort is a pointer sort (see Program 2 in Elementary Data Structures ~ Compound Data Structures). The function takes four arguments: the array; the number of items to be sorted; the size of the items; and a pointer to a function that compares two items, given pointers to them. For example, if Item is char*, then the following code implements a string sort that adheres to our conventions: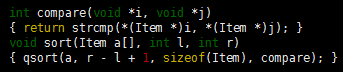
The underlying algorithm is not specified in the interface, but quicksort is widely used. The primary reason to use indices or pointers is to avoid intruding on the data being sorted. We can “sort” a file even if read-only access is all that is available. Moreover, with multiple index or pointer arrays, we can sort one file on multiple keys (see Figure 1). This flexibility to manipulate the data without actually changing them is useful in many applications.
A second reason for manipulating indices is that we can avoid the cost of moving full records. The cost saving is significant for files with large records (and small keys), because the comparison needs to access just a small part of the record, and most of the record is not even touched during the sort. The indirect approach makes the cost of an exchange roughly equal to the cost of a comparison for general situations involving arbitrarily large records (at the cost of the extra space for the indices or pointers). Indeed, if the keys are long, the exchanges might even wind up being less costly than the comparisons. When we estimate the running times of methods that sort files of integers, we are often making the assumption that the costs of comparisons and exchanges are not much different. Conclusions based on this assumption are likely to apply to a broad class of applications, if we use pointer or index sorts.
In typical applications, the pointers are used to access records that may contain several possible keys. For example, records consisting of students’ names and grades or people’s names and ages:
Program 2 and 3 provide an example of a pointer sort interface and implementation that can allow us to sort them using either of the fields as key. We use an array of pointers to records, and declare less as a function, rather than a macro. Then we can provide different implementations of less for different sort applications. For example, if we compile Program 3 together with a file containing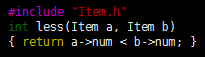
then we get a data type for the items for which any of our sort implementations will do a pointer sort on the integer field. Alternatively, we might choose to use the string field of the records for the sort keys. If we compile Program 3 together with a file containing 
then we get a data type for the items for which any of our sort implementations will do a pointer sort on the string field.
Program 2 Data-type interface for record items
The records have two keys: a string key (for example, a name) in the first field, and an integer key (for example, a grade) in the second field. The comparison less is defined as a function, rather than as a macro, so we can change sort keys by changing implementations,
Program 3 Data-type implementation for record items
These implementations of the ITEMscan and ITEMshow functions for records operate in a manner similar to the string data-type implementation of Program 1, in that they allocate and maintain the memory for the records. We keep the implementation of less in a separate file, so that we can substitute different implementations, and therefore change sort keys, without changing any other code.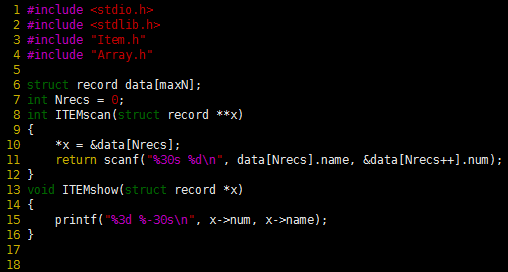
For many applications, the data never need to be rearranged physically to match the order indicated by the indices, and we can simply access them in order using the index array. If this approach is not satisfactory for some reason, we are led to a classic programming exercise: How do we rearrange a file that has been sorted with an index sort? The code
is trivial, but requires extra memory sufficient for another copy of the array. What about the situation when there is not enough room for another copy of the file? We cannot blindly set data[ i ] = data[ a[ i ] ], because that would overwrite the previous value of data[ i ], perhaps prematurely.
Figure 2 illustrates how we can solve this problem, still using a single pass through the file. To move the first element where it belongs, we move the element at that position to where it belongs, and so forth. Continuing this reasoning, we eventually find an element to move to the first position, at which point we have shifted a cycle of elements into position. Then, we move to the second element and perform the same operation for its cycle, and so forth (any elements that we encounter that are already in position (a[ i ] = i ) are on a cycle of length 1 and are not moved).
Specifically, for each value of i, we save the value of data[ i ] and initialize an index variable k to i. Now we think of a hole in the array at i, and seek an element to fill the hole. That element is data[a[ k ]]—in other words, the assignment data[ k ] = data[a[ k ]] moves the hole to a[ k ]. Now the hole is at data[a[ k ]], so we set k to a[ k ]. Iterating, we eventually get to a situation where the hole needs to be filled by data[ i ], which we have saved. When we move an element into position we update the a array to so indicate. Any element in position has a[ i ] equal to i, and the process just outlined is a no-op in that case. Continuing through the array, starting a new cycle each time that we encounter an element not yet moved, we move every element at most once. Program 4 is an implementation of this process.
Figure 2 In-place sort
To rearrange an array in place, we move from left to right, moving elements that need to be moved in cycles. Here, there are four cycles: The first and last are single-element degenerate cases. The second cycle starts at 1. The S goes into a temporary variable, leaving a hole at 1. Moving the second A there leaves a hole at 10. This hole is filled by P, which leaves a hole at 12. That hole is to be filled by the element at position 1, so the reserved S goes into that hole, completing the cycle 1 10 12 that puts those elements in position. Similarly, the cycle 2 8 6 13 4 7 11 3 14 9 completes the sort.
Program 4 In-place sort
The array data[ 0 ], . . . , data[ N – 1 ] is to be rearranged in place as directed by the index array a[ 0 ], . . . , a[ N – 1 ]. Any element with a[ i ] == i is in place and does not need to be touched again. Otherwise, save data[ i ] as v and work through the cycle a[ i ], a[a[ i ]], a[a[a[[[ i ]]], and so on, until reaching the index i again. We follow the process again for the next element which is not in place, and continue in this manner, ultimately rearranging the entire file, moving each record only once.
This process is called in situ permutation, or in-place rearrangement of the file. Again, although the algorithm is interesting, it is unnecessary in many applications, because accessing the data indirectly often suffices. Also, if the records are huge relative to their number, the most efficient option may be simply to rearrange them with a conventional selection sort (see Property 5 in Sorting～Elementary Sorting Methods II).
Indirect sorting requires extra space for the index or pointer array and extra time for the indirect comparisons. In many applications, these costs are a small price to pay for the flexibility of not having to move the data at all. For files consisting of large records, we will almost always choose to use an indirect sort, and for many applications, we will find that it is not necessary to move the data at all. In this series, we normally will access data directly. In a few applications, however, we do use pointers or index arrays to avoid data movement, for precisely the reasons mentioned here.
2、Sorting of Linked Lists
As we know from Elementary Data Structures series, arrays and linked lists provide two of the most basic ways to structure data, and we considered an implementation of insertion sort for linked lists as a list-processing example in Elementary Data Structures ~ Linked Lists II (Program 2). The sort implementations that we have considered to this point all assume that the data to be sorted is in an array, and are not directly applicable if we are working within a system that uses linked lists to organize data. In some cases, the algorithms may be useful, but only if they process data in the essentially sequential manner that we can support efficiently for linked lists.
Program 5 gives an interface, which is similar to Program 3 in Sorting～Elementary Sorting Methods II, for a linked-list data type. With Program 5, the driver program corresponding to Program 2 in Sorting～Elementary Sorting Methods II is a one-liner:
Most of the work (including allocation of memory) is left to the linked-list and sort implementations. As we did with our array driver, we want to initialize the list (either from standard input or with random values), to show the contents of the list, and of course, to sort it. As usual, we use an Item for the data type of the items being sorted, just as we did in Sorting of Other Types of Data in Sorting～Elementary Sorting Methods II. The code to implement the routines for this interface is standard for linked lists of the kind that we examined in detail in Elementary Data Structures series, and left as an exercise.
Program 5 Linked-list-type interface definition
This interface for linked lists can be contrasted with the one for arrays in Program 3 in Sorting～Elementary Sorting Methods II. The init function builds the list, including storage allocation. The show function prints out the keys in the list. Sorting programs use less to compare items and manipulate pointers to rearrange the items. We do not specify here whether or not lists have head nodes.
There is a ground rule for manipulating linked structures that is critical in many applications, but is not evident from this code. In a more complex environment, it could be the case that pointers to the list nodes that we are manipulating are maintained by other parts of the applications system (i.e., they are in multilists). The possibility that nodes could be referenced through pointers that are maintained outside the sort means that our programs should change only links in nodes, and should not alter keys or other information. For example, when we want to do an exchange, it would seem simplest just to exchange items (as we did when sorting arrays). But then any reference to either node with some other link would find the value changed, and probably will not have the desired effect. We need to change the links themselves such that the nodes appear in sorted order when the list is traversed via the links we have access to, without affecting their order when accessed via any other links. Doing so makes the implementations more difficult, but usually is necessary.
We can adapt insertion, selection, and bubble sort to linked-list implementations, although each one presents amusing challenges. Selection sort is straightforward: We maintain an input list (which initially has the data) and an output list (which collects the sorted result), and simply scan through the list to find the maximum element in the input list, remove it from the list, and add it to the front of the output list (see Figure 3). Implementing this operation is a simple exercise in linked-list manipulation, and is a useful method for sorting short lists. An implementation is given in Program 6.
Figure 3 Linked-list selection sort
This diagram depicts one step of selection sort for linked lists. We maintain an input list, pointed to by h->next, and an output list, pointed to by out (top). We scan through the input list to make max point to the node before (and t point to ) the node containing the maximum item. These are the pointers we need to remove t from the input list (reducing its length by 1) and put it at the front of the output list (increasing its length by 1), keeping the output list in order (bottom). Iterating, we eventually exhaust the input list and have the nodes in order in the output list.
Program 6 Linked-list selection sort
Selection sort of a linked list is straightforward, but differs slightly from the array version because it is easier to insert at the front of a list. We maintain an input list (pointed to by h->next), and an output list (pointed to by out). While it is nonempty, we scan the input list to find the maximum remaining element, then remove that element from the input list and insert it at the front of the output list. This implementation uses an auxiliary routine findmax, which returns a link to the node whose link points to the maximum element on a list.
In some list-processing situations, we may not need to explicitly implement a sort at all. For example, we could choose to keep the list in order at all times, inserting new nodes into the list as in insertion sort. This approach comes at little extra cost if insertions are relatively rare or the list is small, and in certain other situations. For example, we might need to scan the whole list for some reason before inserting new nodes (perhaps to check for duplicates).
3、Key-Indexed Counting
A number of sorting algorithms gain efficiency by taking advantage of special properties of keys. For example, consider the following problem: Sort a file of N items whose keys are distinct integers between 0 and N-1. We can solve this problem immediately, using a temporary array b, with the statement
That is, we sort by using the keys as indices, rather than as abstract items that are compared. In this section, we consider an elementary method that uses key indexing in this way to sort efficiently when the keys are integers in a small range.
If all the keys are 0, sorting is trivial, but now suppose that there are two distinct key values 0 and 1. Such a sorting problem might arise when we want to separate out the items in a file that satisfy some (perhaps complicated) acceptance test: we take the key 0 to mean “accept” and the key 1 to mean “reject”. One way to proceed is to count the number of 0s, then to make a second pass through the input a to distribute its items to the temporary array b, using an array of two counters, as follows. We start with 0 in cnt[ 0 ] and the number of 0 keys in the file cnt[ 1 ], to indicate that there are no keys that are less than 0 and cnt [ 1 ] keys that are less than 1 in the file. Clearly, we can fill in the b array by putting 0s at the beginning (starting at b[[cnt[0]], or b[ 0 ]) and 1s starting at b[cnt[ 1 ]. That is, the code 
serves to distribute the items from a to b. Again, we get a fast sort by using the keys as indices (to pick between cnt[0] and cnt[1]). We could use an if statement to choose between the two counters in this simple case, but the approach of using keys as indices generalizes immediately to handle more than two key values (more than two counters).
Specifically, a more realistic problem in the same spirit is this: Sort a file of N items whose keys are integers between 0 and M-1. We can extend the basic method in the previous paragraph to an algorithm called key-indexed counting, which solves this problem effectively if M is not too large. Just as with key values, the idea is to count the number of keys with each value, and then to use the counts to move the items into position on a second pass through the file. First, we count the number of keys of each value: then, we compute partial sums to get counts of the number of keys less than or equal to each value. Then, again just as we did when we had two key values, we use these counts as indices for the purpose of distributing the keys. For each key, we view its associated count as an index pointing to the end of the block of keys with the same value, use the index to distribute the key into b, and decrement. The critical factor that makes this algorithm efficient is that we do not need to go through a chain of if statements to determine which counter to access—using the key as index, we immediately find the right one. This process is illustrated in Figure 4. An implementation is given in Program 7.
Figure 4 Sorting by key-indexed counting.
First, we determine how many keys of each value there are in the file: In this example there are six 0s, four 1s, two 2s, and three 3s. Then, we take partial sums to find the number of keys less than each key: 0 keys are less than 0, 6 keys are less than 1, 10 keys are less than 2, and 12 keys are less than 3 (table in middle). Then, we use the partial sums as indices in placing the keys into position: The 0 at the beginning of the file is put into location 0; we then increment the pointer corresponding to 0, to point to where the next 0 should go. Then, the 3 from the next position on the left in the file is put into location 12 (since there are 12 keys less than 3); its corresponding count is incremented; and so forth.
Program 7 Key-indexed counting
The first for loop initializes the counts to 0; the second for loop sets the second counter to the number of 0s, the third counter to the number of 1s, and so forth. Then, the third for loop simply adds these numbers to produce counts of the number of keys less than or equal to the one corresponding to the count. These numbers now give the indices of the end of the part of the file where keys belong. The fourth for loop moves the keys into an auxiliary array b according to these indices, and the final loop moves the sorted file back into a. The keys must be integers less than M for this code to work, although we can easily modify it to extract such keys from more complex items.
Property 1 Key-indexed counting is a linear-time sort, provided that the range of distinct key values is within a constant factor of the file size.
Each item is moved twice, once for the distribution and once to be moved back to the original array; and each key is referenced twice, once to do the counts and once to do the distribution. The two other for loops in the algorithm involve building the counts, and will contribute insignificantly to the running time unless the number of counts becomes significantly larger than the file size.